Ecuación de la elipse con vértices en los puntos (h, k) y excentricidad e = 2/3

;)
El centro de la elipse seráel punto medio de los vértices:

$$\begin{align}&( \frac{-2+2} 2, 0)=(0,0)\\&\end{align}$$

 No desplazada

Con esos datos hay dos posibilidades. Ya que no indica si esos vértices son los del eje mayor o menor.

Caso1: eje mayor horizontal ==>  a=2 

$$\begin{align}&a=2\\&\\&e= \frac c a\\&\\&\frac 2 3=\frac c a\ ==> c= \frac 2 3 a= \frac 4 3\\&\\&b^2=a^2-c^2=  4-(\frac 4 3)^2=4-\frac {16} 9= \frac{20} 9\\&\\&\frac{x^2}4+ \frac{y^2}{ \frac{20} 9}=1\\&\\&\frac{x^2}{2^2}+ \frac{y^2}{ (\frac{\sqrt{20}} 3)^2}=1\\&\\&\\&\\&\end{align}$$

Caso 2: eje mayor vertical: ==> b=2

$$\begin{align}&\frac{x^2}{b^2}+  \frac{y^2}{a^2}=1\\&\\&\frac{x^2}{2^2}+ \frac{y^2}{a^2}=1\\&\\&e= \frac 2 3= \frac c a\\&\\&a^2=b^2+c^2\\&\\&a^2=4+( \frac 2 3 a)^2\\&\\&a^2=4+ \frac 4 9 a^2\\&\\&9a^2=36+4a^2\\&\\&5a^2=36\\&\\&a^2=\frac {36} 5\\&\\&\frac{x^2}{4}+ \frac{y^2}{ \frac {36} 5}=1\end{align}$$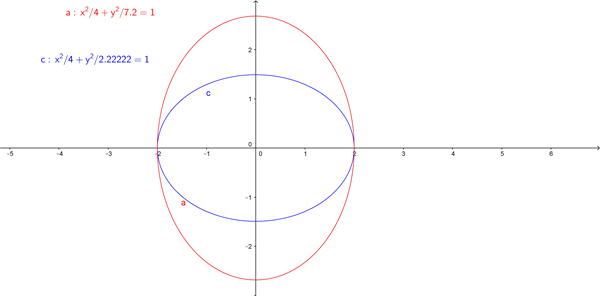

Saludos

;)

;)