¿Cómo analizo el C.V.A de las siguientes proposiciones?
Se que los denominadores no pueden ser cero y los numeradores con raíz par deben ser mayores o iguales a 0,
Pero de ahí, ¿qué más debo analizar para hallar correctamente el C.V.A?
1 Respuesta
;)
Hola Juan pinedo!
El C.V.A.se calcula según el tipo de expresión. Solo has de has de saber que si es:
· un polinomio CVA=R
· un radical de índice impar CVA=R
·un radical de índice par:
$$\begin{align}&f(x)=\sqrt {u(x)} ===> u(x) \geq0\end{align}$$· una fracción algebraica:
$$\begin{align}&f(x)=\frac{P(x)}{Q(x)}\\&\\&CVA= \{x \in \mathbb R/Q(x) \neq0 \}\end{align}$$Las cuatro son correctas
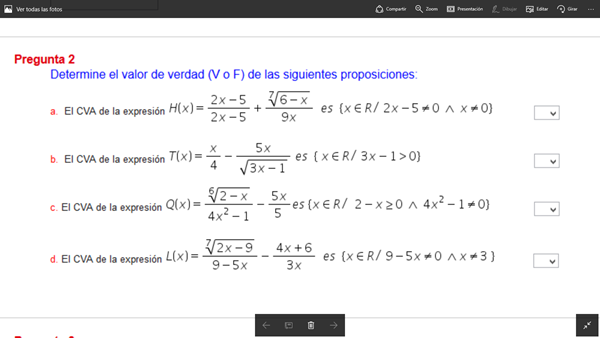
H(x) diferente de 0 los dos denominadores:
$$\begin{align}&2x-5\neq0 \cap x \neq0\end{align}$$T(x) radical de índice par en el denominador ===> 3x-1>0
Q(x) radical de índice par==> 2x-1>0 y denominador diferente de 0
$$\begin{align}& 2x-1>0 \cap 4x^2-1\neq 0\end{align}$$L(x) denominadores diferentes de 0
Todo correcto.
El siguiente paso sería calcular todo eso
Saludos
;)
;)
Gracias, en L(x) porque x no puede ser 3?
;)
Hola Juan!
Lo miré mal:
$$\begin{align}&3x \neq0==> x \neq 0\end{align}$$luego si puede ser 3
Estaría mal L
