Relación de un Punto O exterior al triangulo

;)
Hola David!

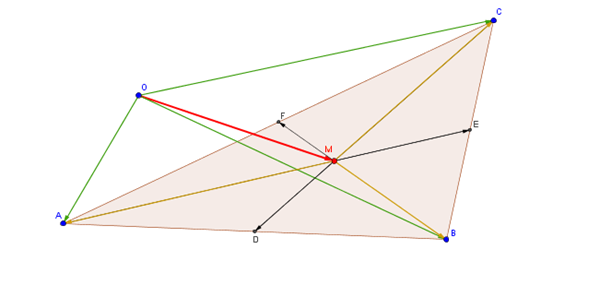
M es el punto de corte de las medianas, luego es el baricentro.

Propiedad del baricentro MB=2 MF

que con vectores:

MB=-2MF

MC=-2MD

MA=-2ME

Por construcción se cumplen las tres igualdades vectoriales:

OM=OA+AM

OM=OB+BM

OM=OC+CM

sumándolas:

3OM=(OA+OB+OC)+(AM+BM+CM)      (*)

la igualdad ha demostrar es equivalente a 3OM=OA+OB+OC

luego estará demostrada si se cumple que la suma vectorial AM+BM+CM=N es (VECTOR NULO)

que equivale, cambiando el sentido de los vectores a: MA+MB+MC= 0

MA+MB+MC=por construcción=(MF+FA)+(MD+DB)+(ME+EC)=

=(MF+MD+ME)+(FA+DB+EC)=MF+MD+ME+ 1/2(CA+AB+BC)    (por hipótesis, puntos medios)=

=MF+MD+ME+ N       (CA+AB+BC es el vector nulo ,ver construcción)

=-1/2 (MB+MC+MA)      (propiedad baricentre)

Si observamos la igualdad obtenida tenemos:

MA+MB+MC= -1/2 (MA+MB+MC)

! O sea, un vector que es igual a la mitad del opuesto. Esto solo lo cumple el vector nulo

luego  MA+MB+MC=N   (vector nulo)

de lo que se sigue:

3OM=OA+OB+OC+ N

3OM=OA+OB+OC

OM=1/3(OA+OB+OC)         

c.q.d.

Como queríamos demostrar

Saludos!

Bonitos problemas

;)

;)