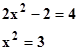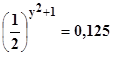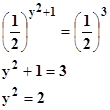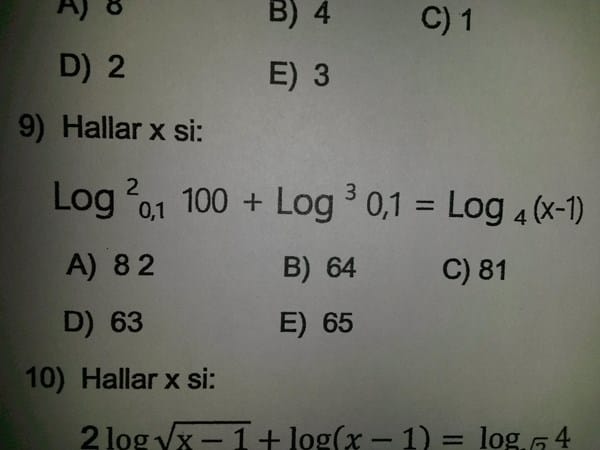Anónimo
No entiendo como resolver estos dos problemas de Logaritmos
Se me hace dificl cuando hay fraciones o exponentes así, y necesito tu ayuda para comprender.
2 Respuestas
Respuesta de Luis Alberto Candio Salcedo
1
Como estas:
Resolvemos el ejercicio N° 3:
Por definición se tiene:
Luego:
Por otro lado:
Resolvemos:
Piden hallar: (x + y)(x - y)
$$\begin{align}&x^2-y^2\end{align}$$Reemplazando:
3 - 2 = 1
Eso es todo, espero puedas entender. No te olvides puntuar la respuesta. Resolvemos un ejercicio por pregunta. Si deseas que te resuelva el otro ejercicio haz de nuevo la pregunta.
Gracias por responder, es necesaria las ayuda si podría ayudarme solo en esta ultima
Respuesta de Valero Angel Serrano Mercadal
1
Hay que usar las propiedades de los logaritmos, en especial para el primero hay que usar esta:
$$\begin{align}&log_a\,a^n =n\\&\\&\text{ya que}\\&\\&log_a\,a^n = n·log_aa= n·1 = n\\&\\&2)\quad \frac{log_264}{log_525}+\frac{log_{\frac 12}\frac 18}{log\,1000}-log_39\times log_{\sqrt 2}4=\\&\\&\frac{log_22^6}{log_55^2}+\frac{log_{\frac 12}\left(\frac 12\right)^3}{log\,10^3}-log_33^2\times log_{\sqrt 2}(\sqrt 2)^4=\\&\\&\frac{6}{2}+\frac{3}{3}-2\times 4=3+1-8=-4\\&\\&\text{La respuesta es la c)}\\&\\&\\&\\&3) \\&\text{Antes de nada fijémonos que}\\&(x+y)(x-y) = x^2-y^2\\&\text{No tenemos porque calcular x y y,}\\&\text{ta vez con sus cuadrados sea suficiente}\\&\\&log_216=2x^2-2\\&log_2\,2^4=2x^2-2\\&4=2x^2-2\\&6=2x^2\\&x^2=3\\&\\&\left(\frac 12 \right)^{y^2+1}=0.125\\&\left(\frac 12 \right)^{y^2+1}=\frac 18 = \left(\frac 12 \right)^3\\&y^2+1 = 3\\&y^2=2\\&\\&(x+y)(x-y)=x^2-y^2=3-2=1\\&\\&\text{La respuesta es la A)}\end{align}$$Y eso es todo, saludos:
:
: