Área entre una curva polar y curva cartesiana

;)
Hola Peri Rockz!

La polar r=2 es una circunferencia de centro el origen de coordenadas y radio 2

Luego tenemos :

Que el área pedida es la de un sector circular, con lo cual se puede calcular directamente sin integrales, buscando el ángulo.

Como tengo un poco de prisa te lo hago así:

Punto de corte:

$$\begin{align}&y=2x\\&x^2+y^2=2^2\\&\\&x^2+4x^2=4\\&5x^2=4\\&\\&x=\frac{2}{\sqrt 5}\\&y=\frac{4}{\sqrt 5}\\&\\&tan \alpha=\frac{y}{x}=2\\&\\&\alpha=arctan2=63.43494882º\\&\\&A= \pi r^2 \frac{\alpha}{360}=4 \pi \frac{63.43494882}{360}=2.214297 \ cm^2\end{align}$$

lo tengo que dejar.

con integrales sería

$$\begin{align}&A= \int_0^{\frac{2}{\sqrt 5}}2xdx+ \int_{\frac{2}{\sqrt 5}}^2 \sqrt{4-x^2} dx\\&\\&circunferencia:\\&x^2+y^2=2^2\end{align}$$

Saludos

;)

;)

·

·

¡Hola Peri!

La curva polar r=2 es una circunferencia centrada en el origen de radio 2. Esta es la gráfica.

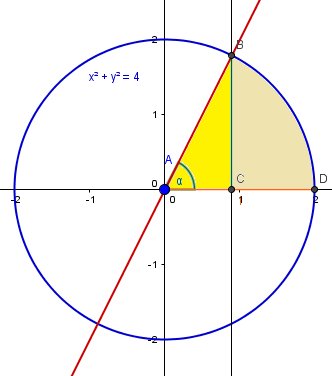
El área se puede calcular como el área de un sector circular. El ángulo alfa es aquel cuya tangente es la pendiente de la recta y=2x

alfa= arctg(2)

Luego el área será:

$$\begin{align}&A= \frac{arctg \,2}{2}·2^2=2\,arctg\,2\approx 2.214297436\,u^2\end{align}$$

No olvidar poner en radianes la calculadora al hacer ese cálculo.

También se puede calcular por integrales, para ello hay que dividir en dos partes la región tal coo he hecho e integrar en cada una.

El punto C de separación de las regiones es la coordenada x de la intersección de las curvas.

La curva polar r=2, como circunferencia centrada en el origen de radio 2 tiene la ecuación cartesiana

x^2+y^2=4

y la recta es

y=2x

sustituyendo en la circunferencia

$$\begin{align}&x^2 + 4x^2 = 4\\&\\&5 x^2=4\\&\\&x=\sqrt{\frac 45}= \frac{2 \sqrt 5}{5}\\&\\&A=\int_0^{\frac{2 \sqrt 5}{5}}2xdx+\int_{\frac{2 \sqrt 5}{5}}^2 \sqrt{4-x^2}dx=\\&\\&x^2\Bigg|_0^{\frac{2 \sqrt 5}{5}}+\int_{\frac{2 \sqrt 5}{5}}^2 \sqrt{4-x^2}dx=\\&\\&\frac{20}{25}+\int_{\frac{2 \sqrt 5}{5}}^2 \sqrt{4-x^2}dx=\\&\\&x=2sen\varphi\implies \varphi=arcsen \frac x2\\&dx=2 \cos \varphi \;d \varphi\\&x=\frac{2 \sqrt 5}{5}\implies\varphi=arc sen \frac{\sqrt 5}{5}\\&x=2\implies\varphi=arcsen\; 1= \frac \pi 2\\&\\&=\frac 45+\int_{arcsen \frac{\sqrt 5}{5}}^{\frac \pi 2}\sqrt{4-4sen^2\varphi}·2 \cos \varphi\;d\varphi=\\&\\&\frac 45+4\int_{arcsen \frac{\sqrt 5}{5}}^{\frac \pi 2} \cos^2\varphi\;d\varphi=\\&\\&\frac 45+4\int_{arcsen \frac{\sqrt 5}{5}}^{\frac \pi 2} \left(\frac 12+\frac{\cos 2\varphi}{2}  \right)\;d\varphi=\\&\\&\frac 45+2\left[\varphi+\frac{sen \,2\varphi}{2}  \right]_{arcsen \frac{\sqrt 5}{5}}^{\frac \pi 2}=\\&\\&\frac 45+2\left(\frac \pi 2+0-arcsen \frac{\sqrt 5}{5}-\frac{sen\left(2arcsen \frac{\sqrt 5}{5}\right)}{2}  \right)=\\&\\&\text{como }sen 2a=2sen\,a·\cos\,a\\&\\&\frac 45+2\left(\frac \pi 2-arcsen \frac{\sqrt 5}{5}-sen\left(arcsen \left( \frac{\sqrt 5}{5}·\sqrt{1-\frac{5}{25}}\right)  \right)  \right)=\\&\\&\frac 45+2\left(\frac \pi 2-arcsen \frac{\sqrt{5}}{5}-\frac{\sqrt{5}}{5}·\frac{\sqrt{20}}{5}  \right)=\\&\\&\frac 45+2\left(\frac \pi 2-arcsen \frac{\sqrt{5}}{5}-\frac{10}{25}  \right)=\\&\\&\frac 45+\pi-2arcsen \frac{\sqrt 5}{5}-\frac 45=\\&\\&\pi-2arcsen \frac{\sqrt 5}{5}\approx 2.214297436u^2\\&\end{align}$$

Que como puedes ver da lo mismo.

He tenido que abreviar algunos pasos porque el editor no puede con tanta fórmula. Estaría bien que la parte del volumen la mandaras en otra pregunta, te lo agradeceríamos mucho, aquí ya se trabajó mucho.

Sa lu dos.

:

: