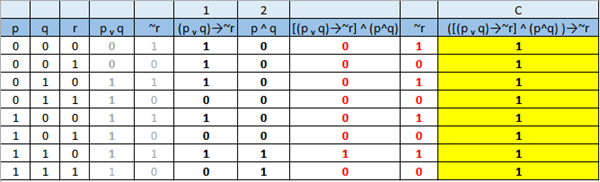
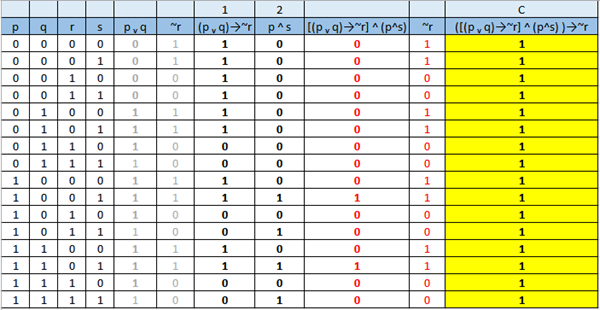
En los numerales ( 6), (7), (8), (9)y (10) identificar todas las expresiones
Identificar todas las expresiones queconsidera son proposiciones lógicas simples y también las expresiones que no sonproposiciones. El siguiente paso es identificar proposiciones compuestas. Paralograr esta identificación, conviene reescribir el texto resaltando los conectivoslógicos que no están explícitos en la expresión. Declarar las proposicionessimples, asignando una de las últimas letras del alfabeto para identificarlas. Finalmente, expresar en lenguaje simbólico las proposiciones simples, compuestas identificadas; y construir sus tablas de verdad. Determinar si la tablade verdad es tautología, contradicción o contingencia.
PROBLEMA:
- Si acepto este trabajo o dejo de practicar el deporte que me apasiona por falta de tiempo, entonces no realizaré mis sueños. He aceptado el trabajo y he dejado de jugar ajedrez. Por lo tanto, no realizaré mis sueños
1 Respuesta
·
·
¡Hola Jhon!
Las proposiciones simples son
p = acepto este trabajo
q = dejo de practicar el deporte que me apasiona por falta de tiempo
r = realizar mis sueños
s = he dejado de jugar al ajedrez.
No está claro si q y s son la misma proposición, podrían serlo pero también podrían no serlo, habría que hablar con él para que lo aclarara. De todas formas cara al resultado final va a dar lo mismo.
Las proposiciones compuestas son.
1) (p v q) ==> ~r
2) p ^ s
C) ~r
De la segunda por simplificación extraemos p, entonces se cumple el antecedente de la primera por cumplikrse una de las dis disyunciones y por lo tanto se cumple el consecuente que era la conclusión del argumento. Por lo tanto el argumento está bien y la tabla tiene que ser una tautología.
En el caso de que ese deporte que le apasiona fuera el ajedrez sobraría la proposición s y las proposiciones compuestas serían
1) (p v q) ==> ~r
2) p ^ q
C) ~r
Que hacen que la conclusión sea la misma incluso con más motivos.
·
¿Tu qué crees? Que debemos suponer que el ajedrez es el deporte que le apasiona, o no.
Espero la aclaración.
:
:
Hola!
No te voy a responder con mucho profesionalismo en lógica porque no se, pero si con sentido de pertenencia y humano.
Si a mi me gustara un deporte en determinado, no lo dejaría de practicar por que tengo que trabajar y cumplir mis sueños, siempre hay tiempo para todo.
Una pregunta:
Si me dices que la tabla de verdad debe dar tautologia. ¿Como quedaría realizada?
Quedo atento, gracias por las ayudas mi estimado.
Lo que yo queria decir es que no han utilizado un lenguaje estricto, de ordenador por ejemplo, y entonces hay ambigüedad en el razonamiento.
Hablan de un deporte que le apasiona y hablan del ajedrez. Yo supongo que son la misma cosa, pero también podrían ser cosas distintas y lo han puesto para que caigamos en la trampa. Por eso que según como lo interpretemos serán 3 ó 4 proposiciones simples. Y por eso estoy en la duda, en estos casos cuando lo haces de una forma te pueden decir que es la otra y viceversa.
Por eso te preguntaba cómo quieres que lo haga.
·
----------------------------
.
A) Suponiendo que el deporte que le apasiona es el ajedrez es:
p = acepto este trabajo
q = dejo de practicar el deporte que me apasiona por falta de tiempo
r = realizar mis sueños
1) (p v q) ==> ~r
2) p ^ q
C) ~r
Y la proposición que se debe comprobar en la tabla es:
([(p v q) ==> ~r] ^ (p ^ q) ) ==> ~r
·
-----------------------------------------------------
.
B) Suponiendo que el deporte que le apasiona pueda no ser el ajedrez.
p = acepto este trabajo
q = dejo de practicar el deporte que me apasiona por falta de tiempo
r = realizar mis sueños
s = he dejado de jugar al ajedrez.
1) (p v q) ==> ~r
2) p ^ s
C) ~r
Y la proposición a demostrar en la tabla es:
([(p v q) ==> ~r] ^ (p ^ s) ) ==> ~r
Y es una tautología porque es todo unos la columna que se demuestra
Y eso es todo.
