Me podríais decir las simetrías de esta función? A mi me sale que es impar.
Haz un estudio de las simetrías que presenta, en caso de que las tenga:
f(x)=5/(x^2-6x+10)
2 Respuestas
Impar no es seguro :) y para confirmarlo calculemos f(-1) y f(1)
f(-1) = 5/((-1)^2-6(-1)+10) = 5/17
f(1) = 5/(1^2-6 (1)+10) = 1
Claramente f(-1) no es -f(1), claramente tampoco es par
Como hay una cuadrática (en el denominador), y una constante, parecería que hay alguna simetria ya que esta función es posible que tenga un máximo (o mínimo) y a partir de ese valor si sea simétrica. Veamos cuando se anula el denominador, ya que eso puede cambiar todo...
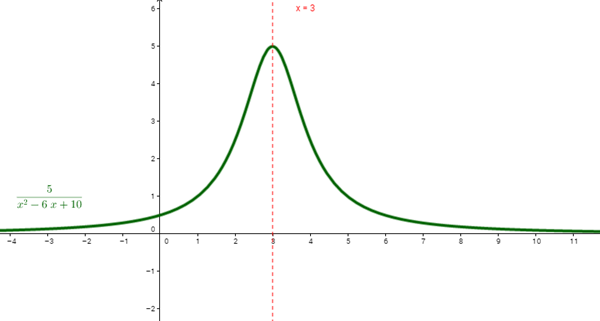
$$\begin{align}&x^2-6x+10 = 0\\&x_{1,2} = \frac{-(-6) \pm \sqrt{(-6)^2-4\cdot 1 \cdot 10}}{2 \cdot 1}=\frac{6\pm \sqrt{-4}}{2}\\&x_{1,2}=3 \pm i\\&\text{No tiene raices, pero el eje x=3 es para estudiar}\\&\text{Busquemos máx/min}\\&f(x) = \frac{5}{x^2-6x+10}\\&f'(x) = \frac{-5 (2x-6)}{(x^2-6x+10)^2}\\&Claramente f'(x)=0 \to x=3\\&f'(2) = 2.5 > 0\\&f'(4) = -2,5 < 0\\& \therefore x=3 \text{ es máximo}\end{align}$$Vemos que en x=3, hay una posible simetría, para verificarlo hagamos
$$\begin{align}&x-3 = u \to x = u+3\\&f(x) = \frac{5}{x^2-6x+10} \to \\&f(u) = \frac{5}{(u+3)^2-6(u+3)+10} = \frac{5}{u^2+6u+9-6u-18+10} = \frac{5}{u^2+1}\\&Resumiendo\\&f(u) = \frac{5}{u^2+1}\\&f(-u)= \frac{5}{(-u)^2+1}=\frac{5}{u^2+1}=f(u) \Rightarrow es\ par\end{align}$$que f(u) sea par, significa que f(x) tiene un eje de simetría en x=3 y te dejo un gráfico de esta función que así lo demuestra.
Lo que no entiendo bien es, cuando ves que no tienes raíces, de donde sacamos que el eje es x=3? y porque pones X(1,2)? Te agradecería me lo explicaras, lo demás lo entiendo todo, gracias.
x=3 sale porque es la parte real de las raíces, pero tienes "varias" formas de darte cuenta de esto (todas equivalentes):
Dado el polinomio ax^2 + bx + c = 0
1. El eje de simetría está en el valor x= - b / (2a)
2. El eje de simetría está en el valor medio entre sus raíces, al tratarse de raíces complejas tendrás que las mismas serán
x_1 = A + B i
x_2 = A - B i
Y cuando hagas el promedio, se anulan los términos imaginarios y "solo" sobrevive A
Respecto a X(1,2), no entiendo a que te refieres, ya que en mi explicación no veo donde usé esa expresión
·
·
¡Hola Mª Antonia!
Yo ya había respondido esa pregunta, aquí está el enlace:
Dominio y simetría de una función
No olvides volver luego aquí para valorar la respuesta.
S a l u d o s
:
: