Geometría analítica.bisectriz entre dos rectas

;)

Hola Juana!

Para calcular la ecuación de la bisectriz de dos rectas has de conocer una propiedad que cumplen todos los puntos de aquella: los puntos de la bisectriz equidistan (están a la misma distancia) de las dos rectas.

Para ello recuerda que la distancia de un punto a una recta es la de la perpendicular (la más pequeña), y que esta se puede calcular con la siguiente fórmula:

$$\begin{align}&r: \ Ax+By+C=0\\&\\&P(x_0,y_0)\\&\\&dist(P,r)=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\\&\\&\end{align}$$

Consideramos el punto P en general P=(x,y) ya que todos los puntos que equidisten de las dos rectas serán de la bisectriz:

$$\begin{align}&dist(P,r)=dist(P,s)\\&\\&\frac{|3x+4y|}{\sqrt{3^2+4^2}}=\frac{|12x+5y-7|}{\sqrt{12^2+5^2}}\\&\\&\frac{|3x+4y|}{5}=\frac{|12x+5y-7|}{13}\\&\\&13|3x+4y|=5|12x+5y-7|\end{align}$$

Las barras verticales significan valor absoluto, ya que una distancia no puede ser negativa.

Al levantar las barras hay dos posibilidades ya que si tenemos por ejemplo

|x|=3

x=3   o  x=-3

Esto traducido a nuestro problema dará lugar a dos ecuaciones (rectas) una será la bisectriz exterior y otra la anterior:

$$\begin{align}&solución1:\\&13(3x+4y)=5(12x+5y-7)\\&39x+52y=60x+25y-35\\&\\&0=21x-27y-35\\&\\&\\&solución2:\\&13(3x+4y)=-5(12x+5y-7)\\&39x+52y=-60x-25y+35\\&\\&99x+77y-35=0\\&\end{align}$$

graficando:

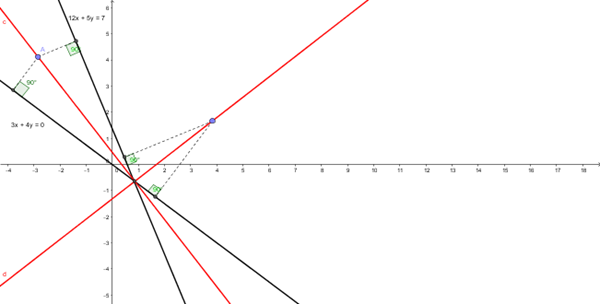
Las líneas rojas son las bisectrices;

Las negras las rectas r i s

Te he dibujado dos distancias de un punto cualquiera a las dos bisectrices. Para un mismo punto la distancia a las dos rectas es la misma

Saludos

;)

;)