Calculo medianas y bario entro de un triangulo
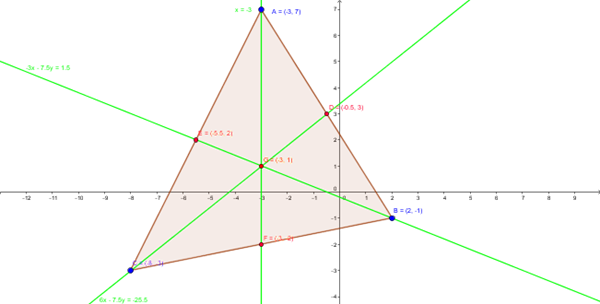
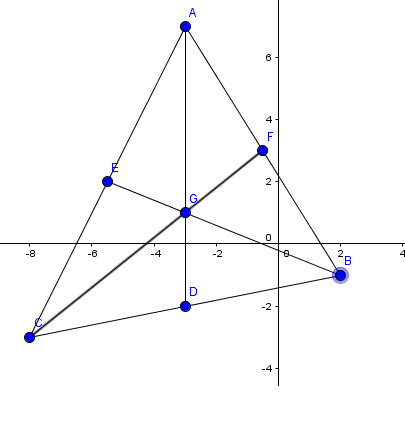
Dado los puntos A(-3,7) B(2,-1)yC(-8,-3) calcular las tres medianas y bario entro. Demostrar que es doble la distancia deA al bario entro que la distancia con punto medio del segmentoBC
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1