Calcular las siguientes integrales por la regla de sustitución:
Me podrían ayudar a resolver estos ejercicios.
Calcular las siguientes integrales por la regla de sustitución:
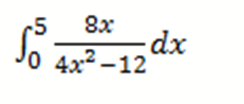
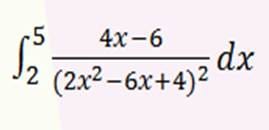
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
