Consulta trigonometría: Hallar los valores de los segmentos indicados con la flechas.
Hallar los valores de los segmentos indicados con la flechas. AC; CZ; YZ.-
BC, CY, YX, XB son iguales.
,XB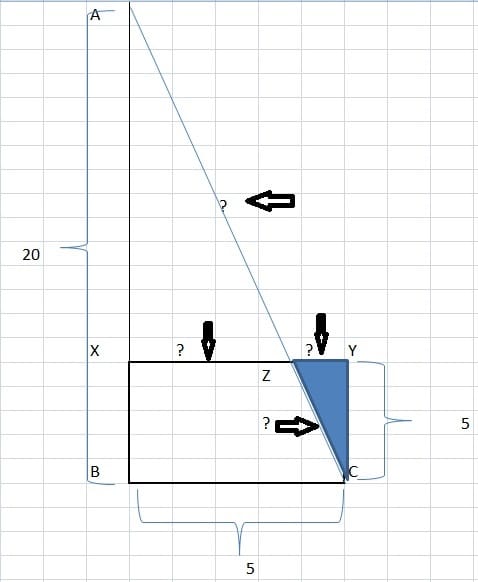
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
