¿Cómo sería la reformulación el método de Runge Kutta para usarlo en INTEGRACIÓN de ecuaciones?

·

·

¡Hola Jesús!

Esto es lo que necesitas para resolverlo sin meterte muy de lleno en la teoría

https://es.wikipedia.org/wiki/M%C3%A9todo_de_Runge-Kutta#M.C3.A9todos_de_Runge-Kutta_de_cuarto_orden 

·

·

En concreto con esto que he capturado es suficiente

Comenzarás con y0=0 e irás calculando sucesivamente y1, y2, yn.

Para ello dividirás el intervalo de integración en n partes, la longitud de cada parte se llama h

h=(b-a)/n

y el valor de xi es

xi = x0+h·i

Una vez has calculado yi, para calcular y(i+1) calculas los valores k1, k2, k3 y k4, nota que para k2 se necesita k1, para k3 se necesita k2 y para k4 se necesita k3

Y luego usas la fórmula que hay para y(i+1)

Una vez hayas llegado a yn tendrás resulelta la integral.

Y eso es todo, espero que te sirva y lo hayas entendido.

Si quieres puedes usar otro método Runge Kuta, pero este ya lo tienes aquí desmenuzado. Si esto tiene una función directa para hacerlo en MathLab es casi seguro pero yo no manejo ese programa.

:

:

Antes que nada: Gracias por tomarte la molestia. A partir de ya; voy a codificar el método numérico y probarlo exhaustivamente. Lo que me llama la atención a primeras de cambio es q: el algoritmo q expones no cambia respecto al RK para solucionar ecuaciones diferenciales ordinarias. Pero déjame trabajarlo y posteriormente me reportaré. X lo pronto: Saludos y buen día (lo q resta de el)

En realidad el método Runge Kutta excede lo que es una simple integral.

En el método Runge Kutta tenemos

dy/dx = f(x,y)

y al hacer la integral definida es

dI(s)/ds = f(s)

Es una función de una sola variable, el valor de la otra da lo mismo cual sea, esto simplifica bastante el calculo de los ki.

Yo he hecho un pequeño programa en C que tú sabrás hacer mucho mejor porque ya de C sé muy poco y en vez de definir la función de dos variables como correspondería a al método RK la he definido solo de una variable. Esta hecho en VisualStudio, imagino que no tendrás problema en adaptarlo al compilador que uses.

#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
double f(double x)
{
    return(4 * pow(x, 3) + 2 * x);
}
int main()
{
    double yi, xi, k1, k2, k3, k4, h, a, b;
    int i, respuesta;
    // string respuesta;
    int n;
    do {
        printf("Limite inferior? : ");
        scanf_s("%lf", &a);
        printf("Limite superior? : ");
        scanf_s("%lf", &b);
        printf("Numero de trozos? : ");
        scanf_s("%d", &n);
        yi = 0;
        h = (b - a) / n;
        printf("h = %lf\n", h);
        for (i = 0; i < n; i++) {
            xi = a + i*h;
            k1 = f(xi);
            k2 = f(xi + h / 2);
            k3 = f(xi + h / 2);
            k4 = f(xi + h);
            yi = yi + (1 / 6.)*h*(k1 + 2 * k2 + 2 * k3 + k4);
        }
        printf("Integral = %lf\n ", yi);
        printf("Otra vez (0=No, 1=Si)? : ");
        scanf_s("%d", &respuesta);
    } while (respuesta == 1);
    return 0;
}

Ahora se ve muy el programa con las indentaciones, ya veremos a ver qué pasa cuando lo envie, porque esta página falla en muchas cosas.

Luego de lo que decía antes la reformaulación consiste en que la función f pasa a depender solo de la primera variable. Y dependiendo del método que uses puedes resumir las operaciones, cosa que yo no hice en el programa pero puedes hacer tú. Por ejemplo, en el que estamos usando resulta que al depender solo de la primera variable tenemos k2=k3

Con lo cual solo habría que calcular k2 y la formula quedaría

$$\begin{align}&y_{i+1}=y_i+\frac 16(k_1+4k_2+k_4)\end{align}$$

Y eso es todo, si tienes alguna duda pregúntame.  Y si no, valora la respuesta.

Saludos.

:

:

¡Gracias!

Efectivamente, la clave de la re formulación estriba en que POR siga siendo la única variable de la que dependa todo el cálculo de la integral, e igualmente se cumple que k2 = k3.

Mis felicitaciones por tu respuesta, muchísimas gracias. Todo quedó muy claro

¡Gracias!

Efectivamente, la clave de la re formulación estriba en que "x" siga siendo la única variable de la que dependa todo el cálculo de la integral, e igualmente se cumple que k2 = k3; sin embargo la contribución de k3 en la fórmula RK de 4o.  orden sigue siendo necesaria.

Mis felicitaciones por tu respuesta, muchísimas gracias. Todo quedó muy claro

Y una vez has comprobado que este método RK4 se transforma en la regla de Simpson cuando quieres hecer una integral definida, lo que puedes hacer si quieres es utilizar la regla de Simpson a la máxima velocidad posible.

#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
double f(double x)
{
    return(4 * pow(x, 3) + 2 * x);
}
int main()
{
    double y1,y2,x1,x2, h, a, b;
    int i, respuesta;
    // string respuesta;
    int n;
    do {
        printf("Limite inferior? : ");
        scanf_s("%lf", &a);
        printf("Limite superior? : ");
        scanf_s("%lf", &b);
        printf("Numero de trozos? : ");
        scanf_s("%d", &n);
        h = (b - a) / n;
        x1 = a;
        x2 = a + h / 2.;
        y1 = 0;
        y2 = 0;
        printf("h = %lf\n", h);
        for (i = 0; i < n; i++) {
            y1 = y1 + f(x1);
            y2 = y2 + f(x2);
            x1 = x1 + h;
            x2 = x2 + h;
        }
        printf("Integral = %lf\n ", (2*y1+4*y2-f(a)+f(x1))*h/6);
        printf("Otra vez (0=No, 1=Si)? : ");
        scanf_s("%d", &respuesta);
    } while (respuesta == 1);
    return 0;
}

Únicamente sería mejorable en tiempo de ejecución  introduciendo la función dentro del propio código en el módulo principal, aunque eso ya me parece excesivo.  Pero sería cuestión de calcular los tiempos si eso fuese algo primordial.

Obsérvese como en la orden final de escritura se suma f(x1) en lugar de f(b), eso por si la suma de n veces h no termina justo en b, siempre es preferible restar una vez lo que se sumó dos veces que restar algo que no se sumó. Una forma más exacta de tomar los puntos sería con

x1=a+i*h 

x2=x1+h/2

pero eso son operaciones más largas que

x1=x1+h

x2=x2+h

Y como estamos trabajando en doble precisión no pienso que haya problemas con lo que he hecho.

Saludos.

:

:

Buen día Sr. Valero, fíjese que me llamó la atención de usar RK 4o. orden reformulado para integrar por que en la ayuda del software LabView comentan que usan éste método para determinar áreas, sin embargo el resultado que muestran; difiere (relativamente) del que uno obtiene, en igualdad de circunstancias usando el mismo método.  

Es seguro que estén añadiendo alguna compensación al error que produce esta formulación.   En fin.

No lo sé, desconozco el software ese. Si acaso es gratis y me dices donde bajarlo para Windows y me dices como hacer una integral con él podría probarlo. Si usan el RK4 o regla de Simpson debería dar el mismo resultado, salvo que por el motivo que sea consideren el doble de intervalos, o utilicen una precisión menor.

En todo caso los resultados de las integrales deberían ser exactos para polinomios de hasta un grado que ahora mismo no te se decir cuál es, con ello se podría probar el orden del método y deducir que no es el método que correspondería.

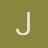
Si, mire LabView es un compilador en el que se codifica de manera gráfica; de tal modo que el "código" de un programa que uno  desarrolle, es en realidad una especie de diagrama de bloques, es decir hay un objeto "gráfico"  para todo lo que se desee programar, desde arreglos numéricos, algoritmos matemáticos, 

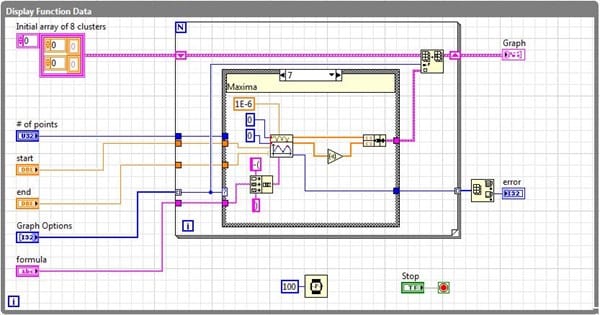
 generadores de gráficas, etc. por mencionar solo algunos.  Y fue desarrollado para que fuera fácilmente programado por Profesionales, sobre todo de la industria con nociones básicas de programación y de este modo pudieran crear programas totalmente funcionales en tiempo récord.

LabView tiene un hermano que se llama LabWindows y este es un compilador de ANSI C (muy bueno, por cierto) y ambos son propiedad de National Instruments.  Una empresa de Hardware y Software muy reputada en el ámbito de las aplicaciones industriales,  National Instruments no tiene un competidor que le espante el sueño en el mundillo Industrial y tiene buen tiempo posicionado en este mercado.

Sus paquetes de Software son bastante caros, hablando de las versiones mas completas y se han constituido como una seria referencia a la hora de apoyarse en los cálculos que ofrecen sus extensas librerías. 

Eso fue, lo que a grandes rasgos podría decirle de LabView.