Geometria analitica. Circunferencias, intersección. CONICAS
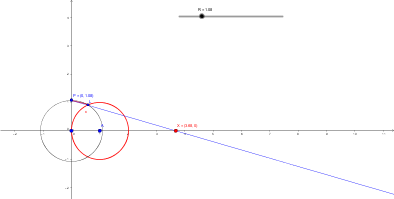
Sea una circunferencia de radio 1 con centro en (1, 0) y una circunferencia de radio R centrada en el origen. Unimos el punto (0, R) con el punto de intersección de las circunferencias (en y > 0) y alargamos el segmento hasta que corte al eje horizontal en X. ¿Qué ocurre con X cuando R se hace más y más pequeño?
2 respuestas
;)
Hola Juana
Cuando R tiende a cero X tiende a 4
Las ecuaciones de las dos circunferencias son:
$$\begin{align}&(x-1)^2+y^2=1\\&\\&x^2+y^2=R^2\\&\\&Buscando \ el \ punto \ de \ corte \ L \ de \ las \ dos \ circunferencias:\\&\\&y^2=R^2-x^2\\&y^2=1-(x-1)^2\\&\\&Igualación: \\&R^2-x^2=1-(x^2-2x+1)\\&R^2=2x\\&x=\frac{R^2}{2} \Rightarrow y^2=R^2-\Big(\frac{R^2}{2} \Big)^2=\frac{4R^2-R^4}{4} \Rightarrow y=\sqrt{\frac{4R^2-R^4}{4}}\\&y=\frac{R}{2} \sqrt{4-R^2}\\&\\&P=(0,R)\\&\\&L=(\frac{R^2}{2},\frac{R}{2} \sqrt{4-R^2})\\&\\&Ecuación\ punto-pendiente \ recta PL:\\&\\&m=\frac{\Delta y}{\Delta x}=\frac{\frac{R}{2} \sqrt{4-R^2}-R}{\frac{R^2}{2}-0}= \frac{R \sqrt{4-R^2}-2R}{R^2}=\\&\\&= \frac{ \sqrt{4-R^2}-2}{R}\\&\\&y-y_o=m(x-x_o)\\&\\&y-R=\frac{ \sqrt{4-R^2}-2}{R}(x-0)\\&\\&y-R=\frac{ \sqrt{4-R^2}-2}{R}x\\&\\&Punto X \ de \ corte \ de \ la \ recta \ PL \ con \ el \ eje \ X \Rightarrow y=0\\&\\&0-R=\frac{ \sqrt{4-R^2}-2}{R}x\\&\\&x=\frac{-R^2}{\sqrt{4-R^2}-2}\\&\\&X=\lim_{R \to 0} \frac{-R^2}{\sqrt{4-R^2}-2}=\frac{0}{0}=\lim_{R \to 0} \frac{-R^2}{\sqrt{4-R^2}-2}·\frac{\sqrt{4-R^2}+2}{\sqrt{4-R^2}+2}=\\&\\&=\lim_{R \to 0} \frac{-R^2(\sqrt{4-R^2}+2)}{(\sqrt{4-R^2})^2-2^2}=\\&\\&=\lim_{R \to 0} \frac{-R^2(\sqrt{4-R^2}+2)}{4-R^2-4}=\\&\\&=\lim_{R \to 0} \frac{-R^2(\sqrt{4-R^2}+2)}{-R^2}=\\&\\&=\lim_{R \to 0} (\sqrt{4-R^2}+2)=2+2=4\\&\\&\\&\end{align}$$;)
;)
·
·
¡Hola Juana!
Las ecuaciones de las dos circunferencias son:
$$\begin{align}&(x-1)^2+y^2=1\implies y^2=1-x^2+2x-1\implies y^2=-x^2+2x\\&\\&x^2+y^2=R^2\implies y^2=R^2-x^2\\&\\&\text{igualando tenemos}\\&-x^2+2x=R^2-x^2\\&\\&2x= R^2\\&\\&x= \frac {R^2}2\\&\\&y =\sqrt{R^2-\frac{R^4}{4}}=\sqrt{\frac{4R^2-R^4}{4}}=\frac{R \sqrt{4-R^2}}{2}\\&\\&\text{La ecuación de la recta de (0,R) a ese punto será}\\&\\&y=y_0+m(x-x_0)\\&\\&y = R+\frac{\frac{R \sqrt{4-R^2}}{2}-R}{\frac{R^2}{2}}(x-0)\\&\\&y=R+\frac{R \sqrt{4-R^2}-2R}{R^2}x=R+\frac{\sqrt{4-R^2}-2}{R}x\\&\\&\text{El corte con el eje X es}\\&\\&0=R+\frac{\sqrt{4-R^2}-2}{R}x\\&\\&x =\frac{-R}{\frac{\sqrt{4-R^2}-2}{R}}=-\frac{R^2}{\sqrt{4-R^2}-2}\\&\\&\text{Ese es el punto que nos piden, el límite cuando } R \to 0 \\&\\&\lim_{R\to 0}\frac{-R^2}{\sqrt{4-R^2}-2}=\lim_{R\to 0}\frac{-R^2(\sqrt{4-R^2}+2)}{4-R^2-4}=\\&\\&\lim_{R\to 0}\frac{-R^2(\sqrt{4-R^2}+2)}{R^2}=\lim_{R\to 0}(\sqrt{4-R^2}+2)=\\&\\&2+2=4\end{align}$$Luego el punto de corte con el eje X tiende a 4.
:
:
Aún no saben ,imites..se podría resolver sin usar eso.?
Es un problema de cálculo de límites descarado. Si al sustituir R=0 en la fórmula del valor x nos diera un número concreto, te diría que se puede resolver sin límites, pero da un 0/0, para resolverlo hay que usar técnicas de cálculo de límites por fuerza.