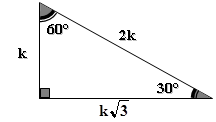
Relación entre tangente de 30 y cotangente de 60
En ángulos complementarios la tangente de uno es la cotangente del complementario.. Sin embargo no obtengo esos resultados al calcularlos.. Algo hago mal.
2 respuestas
·
·
¡Hola Juana!
Los ángulos complementarios intercambian el seno y el coseno, es decir
sen(alfa) = cos(90-alfa)
cos(alfa) = sen(90-alfa)
Eso lo puedes comprobar sobre la circunferencia unidad viendo que al tomar el ángulo complementario tienes en vertical lo mismo que con el otro era horizontal y viceversa. O por definición tomando un triángulo rectángulo.
sen(alfa) = (lado opuesto) / hipotenusa
Pero si tomas el otro ángulo que es 90-alfa el lado tomadao ahí ahora será el adyacente al ángulo
cos(90-alfa) = (mismo lado de antes) / hipotenusa
luego
sen(alfa) = cos(90-alfa)
Y entonces tendremos
$$\begin{align}&tg\, 30º=\frac{sen \,30º}{\cos 30º}=\frac{\cos(90º-30º)}{sen(90º-30º)}=\frac{\cos 60º}{sen\, 60º}=ctg\,60º\end{align}$$Luego son iguales.
Saludos.
:
:
Mi problema era calculadora al hacer cotangente
La cotangente no la tienes en la calculadora. La puedes calcular de dos formas
1/tg(60)
O calcular tg(60) y después dar a la tecla x^-1