Coseno de 72 grados sin calculadora
Como se puede calcular el coseno de 72 grados a partir de un triangulo isósceles
2 respuestas
·
·
¡Hola Juana!
No creo yo que estés estudiando ese tipo de geometría que ha usado Lucas, mas bien trigonometría normal.
Si formamos el triángulo isósceles tendremos estos ángulos
A) 72º
B) 72º
C) 180 - 72º - 72º = 180º - 144 º = 36º
Si aplicamos el teorema de los senos tendremos
$$\begin{align}&\frac{a}{sen A}=\frac{c}{senC}\\&\\&\text{Hagamos el triángulo de tal forma que a=1}\\&\\&\frac{1}{sen 72º}= \frac{c}{sen36º}\\&\\&c=\frac{sen36º}{sen72º}\\&\\&\text{por una identidad trigonométrica}\\&\\&c=\frac{sen 36º}{2sen36º·cos36º}= \frac 1{2cos36º}\\&\\&\cos 36º = \frac 1{2c}\\&\\&\text{Por otro lado el teorema de los cosenos dice}\\&\\&c^2 = 1^2+1^2-2·1·1·cos36º\\&\\&c^2=2-2cos36º\\&\\&cos36º=\frac{2-c^2}{2}\\&\\&\text{Igualando las dos expresiones que tenemos}\\&\\&\frac{1}{2c}=\frac{2-c^2}{2}\\&\\&4c-2c^3=2\\&\\&2c^3-4c+2=0\\&\\&\text{se ve claro que c=1 es una raíz}\\&\text{dividiendo por ruffini tenemos}\\&\\&(2c^2+2c-2)(c-1)=0\\&(c^2+c-1)(c-1)=0\\&\\&\text{Si c=1 son todos los lados iguales, no sirve}\\&\\&c=\frac{-1\pm \sqrt{1+4}}{2}\\&\\&\text{la respuesta negativa tampoco sirve}\\&\\&c=\frac{-1+\sqrt 5}{2}\\&\\&\text{Dado que a=1 entonces }cos72º=\frac c2\\&\\&cos72º = \frac{-1+\sqrt 5}{4}\approx 0.3090169944\end{align}$$:
:
Mi pregunta es que hemos supuesto los dos lados del triangulo 1 eso es válido... ¿en en caso de todos los demás triángulos que no cumplieran esta condición de partida?
No nos dicen que los lados tengan que tener una mediada determinada.
He elegido que ese la do mida 1 para simplificar las cuentas, del mismo modo que las funciones trigonométricas se estudian sobre la circunferencia de radio 1.
Si en vez de tomar ese lado de medida 1 lo tomas de medida r lo que obtendras al final que c mide r veces lo que nos dio ahora. Todo eso lo puedes comprobar fácilmente.
Y al final el coseno sera el cociente de del lado adyacente entre la hipotenusa.
(cr/2)/r =c/2
Que es lo mismo.
Saludos.
·
·
Me explicas lo del cociente adyacente.por favor
Si tu tomas un triángulo rectangulo y tomas uno de los ángulos que no sea el de 90, entonces ese ángulo tiene un cateto que toca ese vértice, ese es el lado adyacente, mientras que el otro cateto no lo toca y es el opuesto. Y luego está también la hipotenusa.
Con todo ello tenemos que para ese ángulo, llamémoslo alfa, las relaciones trigonométricas son:
sen(alfa) = (cateto opuesto) / hipotenusa
cos(alfa) = (cateto adyacente) / hipotenusa
tg(alfa) = (cateto opuesto) / (cateto adyacente)
Si el ángulo alfa es que forma el suelo y la hipotenusa, el cateto adyacente será el horizontal y el opuesto el vertical. Si es el que forma la pared con la hipotenusa es al revés.
Saludos.
:
.
Para encontrar ese valor has de conocer unos resultados de la geometría clásica: el triángulo áureo y la proporción áurea
El triángulo áureo aparece en el pentágono regular y ya los griegos(Los Pitagóricos) sabían que la razón entre la diagonal (d) y el lado (c) de un pentágono regular es la razón áurea.
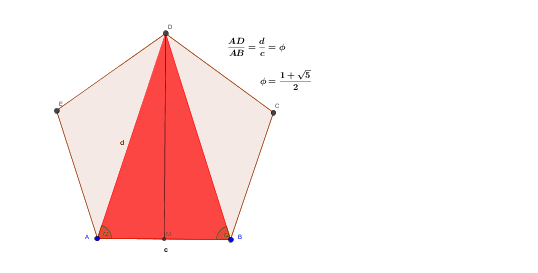
La razón áurea, o proporción áurea o número áureo se representa con la
Letra griega phi. Cuando dos segmentos están en proporción áurea la razón de sus longitudes es phi.
El triángulo isósceles de ángulos 72º, 72º y 36º se llama triángulo áureo, aparece en el pentágono regular y por lo tanto sabemos que
d/c= phi
$$\begin{align}&\phi=\frac{1+\sqrt 5}{2}\end{align}$$Utilizando la mitad de ese triángulo : AMD
$$\begin{align}&cos72º=\frac{\frac{c}{2}}{d}=\frac{c}{2d}=\frac{1}{2 \phi}\\&\\&\frac{1}{\phi}=\frac{2}{1+ \sqrt 5}= Racionalizando=\\&\\&=\frac{2}{\sqrt 5 +1}· \frac {\sqrt 5 -1}{\sqrt 5 -1}=\frac{2(\sqrt 5 -1)}{\sqrt 5^2-1^2}=\frac{2(\sqrt 5 -1)}{4}\\&\\&\\&\cos 72º=\frac{1}{2 \phi}=\frac{1}{2}·\frac{1}{\phi}=\frac{1}{2}·\frac{2(\sqrt 5 -1)}{4}=\frac{\sqrt 5-1}{4}\simeq0,309016994\end{align}$$Espero que te guste la geometría
Saludos
;)
;)
Gracias peroese valor de raíz de 5 más uno..de donde sale???????