Planteamiento y la solución del siguiente problema deLógica Proposicional:
Buenas tarde señores de todo expertos les agradezco su ayuda con este ejercicio espero me ayuden ya que no me cuadran muy bien la proporciones
1 respuesta
Maestro interpretemos desde el punto de vista que 4,3 fue que aprobó todas las materias
Tomemos las proposiciones simples
p = Soraida estudia electrónica
q = Participar en la convocatoria laboral de ...
r = Aprobar telemática
s = Aprobar microcontroladores.
Las proposiciones compuestas son:
a) p => q
b) (¬r ^ ¬s) => ¬q
c) (r v s) => q
d) q <=> (r ^s)
Y la que debemos demostrar es
(a^b^c) => d
como ayuda llamaremos e = (a^b^c) luego será demostrar
e => d
Yo no estoy seguro si la p habría que darla siempre por cierta, el hecho de que no vuelva a aparecer parece querer decir que es algo que se cumple siempre. Y es que así con 3 proposiciones en vez de 4 serían 8 posibilidades en vez de 16
La tabla de la verdad será esta:
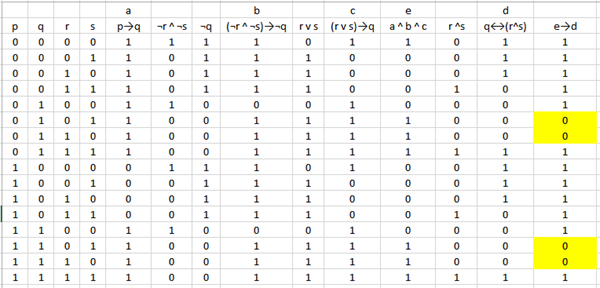
Como puede verse es una contingencia ya que se dan verdaderos y falsos
Se dan falsos cuando va a la convocatoria y una de las dos está aprobada y la otra no. Lo cual podría haberse visto sin necesidad de hacer las tablas, es que yo pensaba que había que hacerlas porque en otros ejercicios me decían que había que hacerlas.
Las proposiciones c y d son contradictorias
La c dice que se va a la convocatoria aprobando una de las dos.
La d dice que se va solo si se han aprobado las dos.
:
:
