Hallar el centroide de la región limitada por la curva

·

·

¡Hola Oscar!

La fórmula para hallar en centroide de una figura plana es:

$$\begin{align}&x_c=\frac{\iint_Ax\,\gamma(x,y)dx\,dy}{\iint_A\gamma(x,y)dx\,dy}\\&\\&y_c=\frac{\iint_Ay\,\gamma(x,y)dx\,dy}{\iint_A\gamma(x,y)dx\,dy}\\&\\&\text{Donde }\gamma(x,y)\text{ es la función de densidad}\\&\text{Si la densidad es constante}\\&\\&x_c=\frac{\iint_Ax\,dx\,dy}{\iint_Adx\,dy}\\&\\&y_c=\frac{\iint_Ay\,dx\,dy}{\iint_Adx\,dy}\\&\end{align}$$

Calculemos los límites de integración de las integrales dobles, para ello calculamos los puntos de intersección en x

x^2 = x+2

x^2 - x - 2 = 0

(x+1)(x-2) = 0

Luego son los puntos x=-1 y x=2 

Como solo hay dos intersecciones y las curvas son continuas la región que determinan tiene un solo trozo, se calcula la integral de una sola vez.

Es conveniente saber cuál es la función superior e inferior en ese intervalo, por ejemplo para x=0

y=x^2 = 0^2 = 0

y=x+2 = 0+2 = 2

luego y=x+2 es la superior y y=x^2 la inferior.

Así la integral del área  es:

$$\begin{align}&\int_{-1}^2\int_{x^2}^{x+2}dydx=\\&\\&\int_{-1}^2(x+2-x^2)dx=\\&\\&\left[\frac{x^2}{2}+2x-\frac{x^3}{3}  \right]_{-1}^2=2+4-\frac 83-\frac 12+2-\frac 13=\\&\\&8-3-\frac 12=\frac 92\\&\\&\text{Y las integrales de los numeradores son}\\&\\&\\&\int_{-1}^2\int_{x^2}^{x+2}x\;dydx=\int_{-1}^2xy\bigg|_{x^2}^{x+2}\;dx=\\&\\&\int_{-1}^2x(x+2-x^2)dx=\\&\\&\int_{-1}^2(x^2+2x-x^3)dx=\\&\\&\left[\frac{x^3}{3}+x^2-\frac{x^4}{4}  \right]_{-1}^2\\&\\&\frac 83+4-4+\frac 13-1+\frac 14=-1+3+\frac 14=\frac 94\\&\\&x_c=\frac{\frac{9}{4}}{\frac 92}=\frac 12\\&\\&\\&\\&\int_{-1}^2\int_{x^2}^{x+2}y\;dydx=\int_{-1}^2 \frac{y^2}{2}\bigg|_{x^2}^{x+2}dx=\\&\\&\frac 12\int_{-1}^2\left((x+2)^2-x^4\right)dx=\\&\\&\frac 12\int_{-1}^2(x^2+4x+4-x^4)dx=\\&\\&\frac 12\left[\frac{x^3}{3}+2x^2+4x-\frac{x^5}{5}  \right]_{-1}^2=\\&\\&\frac 12\left(\frac 83+8+8-\frac {32}5+ \frac 13-2+4-\frac 15  \right)=\\&\\&\frac 12\left(3+18-\frac {33}5  \right)=\frac 12 \frac {72}5=\frac {36}5\\&\\&y_c=\frac{\frac{36}{5}}{\frac 92}=\frac{36·2}{5·9}=\frac{4·2}{5}=\frac{8}{5}\\&\\&\\&\text{Luego el centroide es }\\&\\&(x_c,y_c)=\left(\frac 12,\; \frac 85  \right)\\&\\&\end{align}$$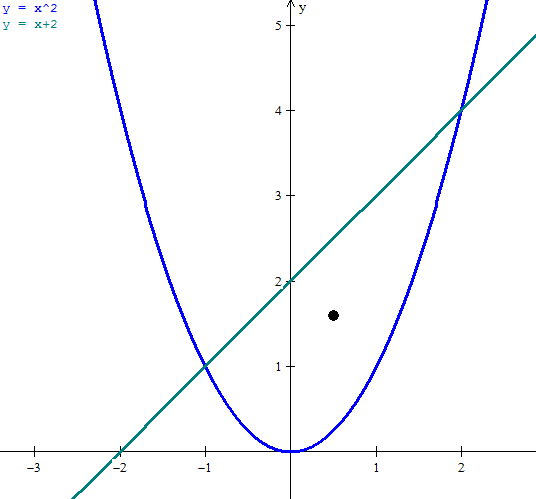

:

: