Necesito resolver esta tarea de matematicas
Necesito hallar el dominio y rango y despejar X de estas funciones:
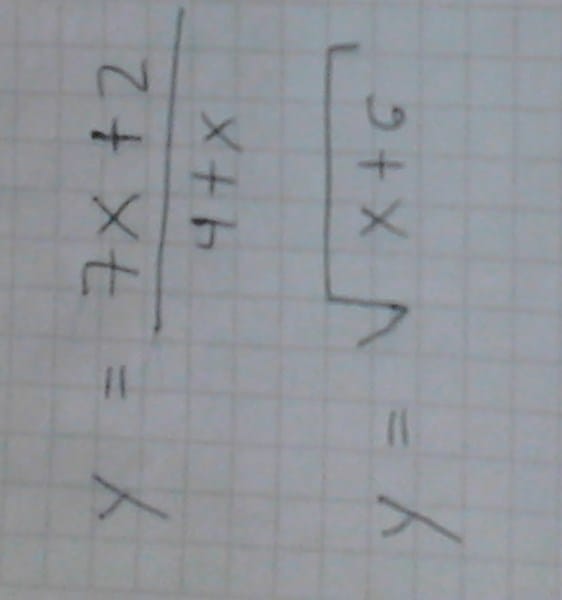
Los necesito con el procedimiento.
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
