Realiza el siguiente problema de optimización
Una compañía va a elaborar cajas rectangulares de fondo cuadrado (paralelepípedo rectangular).
Obtener el costo mínimo del material, si las paredes cuestan $3 cada metro cuadrado, el piso y el techo $7 el metro cuadrado y la caja debe tener 3m^3 de volumen.
*Plantear función del costo y grafica
1 Respuesta
Respuesta de Lucas m
Sea x el lado del cuadrado, y h la altura:
El coste de la base es 7x^2
El coste de la cara lateral es 3xh
Hay dos bases y cuatro caras laterales:
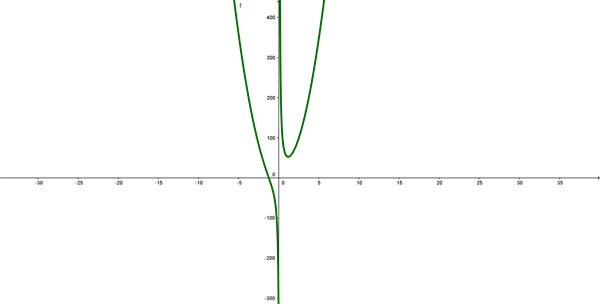
$$\begin{align}&C(x,h)=2(7x^2)+4(3xh)=14x^2+12xh\\&\\&V=3=x^2h \Rightarrow h= \frac{3}{x^2} \Longrightarrow\\&\\&C(x)=14x^2+12x \frac{3}{x^2}= 14 x^2 +\frac{36}{x}=\frac{14x^3+36}{x}\\&\\&C'(x)=\frac{42x^2·x-(14x^3+36)1}{x^2}=\frac{28x^3-36}{x^2}\\&C'(x)=0 \Rightarrow 28x^3-36=0 \Rightarrow x= \sqrt[3] \frac{36}{28}=\sqrt[3] \frac{9}{7} \simeq 1.08 \ m\\&\\&Comprobación \ mínimo:\\&C'(1)=\frac{28-36}{1}<0 \Rightarrow decreciente\\&C'(2)=\frac{24·2^3-36}{2^2}>0 \Rightarrow creciente\\&Luego \ x=\sqrt[3] \frac{9}{7} \simeq 1.08 \ m \ es \ un \ mínimo\\&\\&C(\sqrt[3] \frac{9}{7})=\frac{14·\frac{9}{7}+36}{\sqrt[3] \frac{9}{7}}=54 \sqrt[3] \frac{7}{9} \simeq 49.66 \ $\end{align}$$Graficando C(x):
