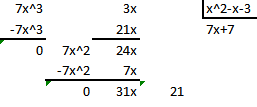No entiendo esta integral, como la realizo

$$\begin{align}& \end{align}$$

·

·

¡Hola Brenda!

Lo primero es que el numerador debe tener grado menor que el del denominador. Para conseguirlo haremos la división de polinomios y obtendremos el cociente y el resto, el cociente quedará como tal y el resto dividido por el divisor

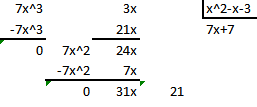
$$\begin{align}&I=\int \frac{7x^3+3x}{x^2-x-3}dx=\\&\\&\int \left(7x+7+\frac{31x+21}{x^2-x-3}\right)dx=\\&\\&\frac{7x^2}{2}+7x+\int \frac{31x+21}{x^2-x-3}dx=\\&\\&\text{Hay que hallar las raíces del denominador}\\&\\&x=\frac{1\pm \sqrt{1+12}}{2}=\frac{1\pm \sqrt{13}}{2}\\&\\&\text{hay que descomponer en fracciones simples}\\&\\&\frac{31x+21}{x^2-x-3}=\frac{a}{x-\frac{1+ \sqrt{13}}{2}}+\frac {b}{x-\frac{1- \sqrt{13}}{2}}=\\&\\&\frac{(a+b)x-\frac {a+b}2+\frac{(a-b)\sqrt{13}}{2}}{x^2-x-3}\\&\\&luego\\&\\&a+b=31  \implies a=31-b\\&\\&-\frac {a+b}2+\frac{(a-b)\sqrt{13}}{2}=21\\&\\&-(a+b)+(a-b) \sqrt{ 13}=42\\&\\&-31+(31-b-b) \sqrt {13}=42\\&\\&(31-2b)\sqrt {13}=73\\&\\&31-2b=\frac{73}{\sqrt {13}}=\frac{73 \sqrt {13}}{13}\\&\\&2b=31 -\frac{73 \sqrt {13}}{13}=\frac{403+73 \sqrt {13}}{13}\\&\\&b=\frac{403-73 \sqrt {13}}{26}\\&\\&a=31-\frac{403-73 \sqrt {13}}{26}=\frac{403+73 \sqrt {13}}{26}\\&\\&I=\frac{7x^2}{2}+7x+\frac{403+73 \sqrt {13}}{26}\int \frac{dx}{x-\frac{1+ \sqrt{13}}{2}}+\frac{403-73 \sqrt {13}}{26}\int \frac{dx}{x-\frac{1- \sqrt{13}}{2}}=\\&\\&\frac{7x^2}{2}-7x+\frac{403+73 \sqrt {13}}{26}ln \bigg|x-\frac{1+ \sqrt{13}}{2}\bigg|+\frac{403-73 \sqrt {13}}{26}ln \bigg|x-\frac{1- \sqrt{13}}{2}\bigg|+C=\\&\\&\text{los ln2 que van a quedar son constantes que se meten en C}\\&\\&\frac{7x^2}{2}-7x+\frac{403+73 \sqrt {13}}{26}ln \bigg|2x-1- \sqrt{13}\bigg|+\frac{403-73 \sqrt {13}}{26}ln \bigg|2x-1+ \sqrt{13}\bigg|+C\\&\end{align}$$