Estudio de Función. Dada f(x)= |x+1|-2 determinar:

Ahora me doy cuenta que no hice muy bien el problema.

En la parte b) contesté f(-1) + f(f(-2))

y en realidad pedían

f(-1) + f(f(2)) =

|-1 + 1|- 2 + ||2+1|-2 +1|- 2 =

0 - 2 + ||3|-1|- 2 =

- 2 + 2 - 2 = -2

Aunque puede ser más sencillo como te lo ha hecho Ninel en tres pasos

f(-1) = |-1+1| - 2 = -2

f(2) = |2+1|-2 = 3-2 = 1

f(f(2)) = f(1) = |1+1|-2 = 0

Luego

f(-1) + f(f(2)) = -2 + 0 = -2

·

Y el apartado c) se me olvidó hacer una simplificación final

f(x^2) = |x^2 + 1| - 2 = x^2 + 1 - 2 = x^2 - 1

·

Muy bien respondido Ninel.

a) El dominio de una función, es el conjunto de número x, reales, donde la expresión:

f(x) = |x+1| - 2

Tiene sentido; esto es, donde la función está bien definida.

Como la expresión |x+1|-2 tiene sentido para todo x en los reales, tenemos que el dominio de ésta función es el conjunto de todos los números reales.

No se a qué te refieres con "origen". Me pregunto si será más bien determinar la imagen de la función. Es lo que voy a hacer. Si no es la imagen, me lo especificas bien, para entender qué te están pidiendo.

La imagen de la función es el conjunto de todos los valores

y = f(x) = |x + 1| - 2

Que puede tomar la función, sabiendo que x varía en los números reales.

Recuerda que el valor absoluto de cualquier número siempre es mayor o igual que cero. Entonces tenemos que:

 0 ≤ |x + 1|

Restando 2 de ambos lados de la desigualdad, nos queda:

-2 ≤ |x + 1| - 2 = f(x)

Así que la función toma todos los valores mayores o iguales que -2.

Por lo tanto la imagen de la función es el intervalo [-2, ∞).

Para la gráfica.

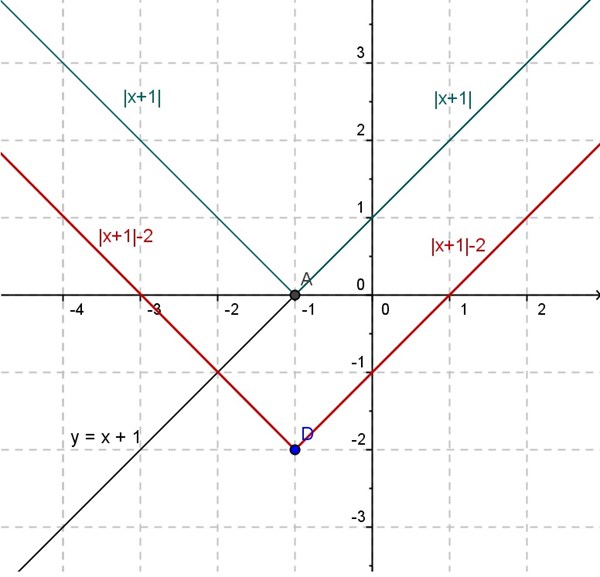
Puedes trazar la recta y = x + 1, que es como la identidad (recta que pasa por el origen y forma un ángulo de 45 grados con los ejes), pero trasladada una unidad hacia arriva (verticalmente). Corta al eje Y en el punto (0,1) y al eje X en el punto (-1,0).
Luego, al sacar valor absoluto de x + 1, la parte de la recta y = x+1 que queda por abajo del eje X, se refleja hacia la parte de arriba. Te va a quedar como una V con el vértice en el punto (-1,0). Esta será la gráfica de y = |x+1|.

Por último, al restar la constante 2, toda la gráfica se traslada verticalmente, hacia abajo dos unidades. Es la misma V, pero con vértice en el punto (-1,-2).

Como se muestra en la figura:

b) Para calcular f(-1) + f(f(2)). Calculamos primero:

f(2) = |2+1|-2 = |3| - 2 = 3 - 2 = 1. Por tanto f(2) = 1

Ahora aplicamos f   a    f(2) = 1:

f((2)) = f(1) = |1+1|-2 = |2|-2 = 2 - 2 = 0

Ahora calculamos f(-1) = |-1+1|-2 = 0-2 = -2

[Me confundió un poco el resultado del profesor Valero, pero hay un error en el tercer renglón de lo que escribió, cuando calcula los valores absolutos de su segundo renglón, debió quedarle: -2 + |-2| -2 = -2 + 2 -2 = -2; de todos modos su procedimiento es correcto y se llega al mismo resultado]

Y sumamos:

f(-1) + f(f(2)) = -2 + 0 = -2.

c) Es la composición de la función f con g, donde f se aplica a los valores que toma la función g:

f(g(x)) = |g(x) + 1| - 2 = |x^2 + 1| - 2

Como el cuadrado de un número siempre es mayor o igual que cero, tenemos que:

x^2 + 1 es mayor que cero, de forma que su valor absoluto es el mismo; y, nos va a quedar:

|x^2 + 1| - 2 = x^2 + 1 - 2 = x^2 - 1

Por tanto f(g(x)) = x^2 - 1