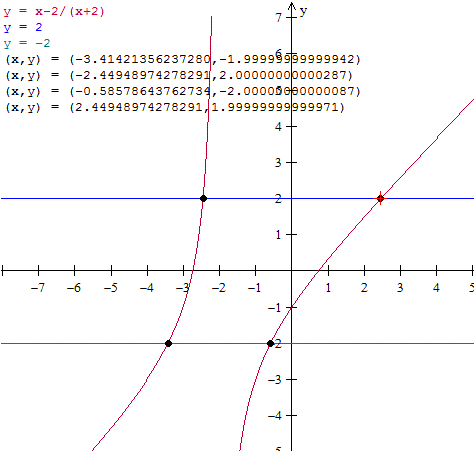Anónimo
Ejercicio de valor absoluto
Hola valeroasm tengo una desigualdad con valor absoluto bastante complicado y pues.... No he podido solucionarlo , necesito que me colabores y me trates de explicar paso a paso como se llega a su solución. Es este:
| x- (2/(x+2)) | > 2
De antemano muchas gracias y espero que me puedas ayudar a entenderlo.
1 respuesta
Para no tener que pegarme con el corrector ortográfico usaré z en lugar de equis.
Una desigualdad o igualdad de este tipo se descompone en estas dos:
1) z - 2/(z+2) > 2
2) z - 2/(z+2) < -2
Hagamos la primera
1) z - 2/(z+2) > 2
z - 2 > 2/(z+2)
Ahora hay que considerar dos casos,
1a) Si z+2 > 0 puede pasar el denominador al otro lado sin cambiar la desigualdad
(z-2)(z+2) > 2
z^2 - 4 > 2
z^2 > 6
z > sqrt(6) o z < -sqrt(6)
Pero si tomamos la segunda opción, como
sqrt(6) = 2,4495 ==>
z < -sqrt(6 = -2,4495 ==>
z+2 < -2,4495 + 2 = -o,4495
Pero esto está en contradicción con la suposición z+2>0, luego la solución 1a) es
z>sqrt(6)
1b) Si z+2 < 0 se pasa el denominador cambiando el sentido de la desigualdad
(z-2)(z+2) < 2
z^2 - 4 < 2
z^2 < 6
-sqrt(6) < z < sqrt(6)
pero por otro lado la suposición z+2<0 es lo mismo que
z<-2
Y reuniendo las dos queda que la solución para 1b) es
-sqrt(6) < z < -2
2) Resolvemos la desigualdad segunda
z - 2/(z+2) < -2
z+2 < 2/(z+2)
De nuevo se descompone en dos casos
2a) si z+2>0 pasamos el denominador al otro lado sin cambiar la desigualdad
(z+2)(z+2) < 2
-sqrt(2) < (z+2) < sqrt(2)
-sqrt(2)-2 < z < sqrt(2) -2
Pero lo suposición era z+2>0 ==> z>-2, luego debemos recortar el intervalo y queda
-2< z < sqrt(2)-2
2b) Si z+2 < 0 se pasa el denominador al otro lado cambiando la desigualdad
(z+2)(z+2) > 2
Esto significa las dos desigualdades de abajo
z+2 > sqrt(2) o
z+2 < -sqrt(2)
Pero la primera es incompatible con z+2< 0
La segunda es totalmente compatible
Luego la solución para 2b) es:
z < -2-sqrt(2)
Y la solución completa es la unión de las soluciones:
sqrt(6) < z
-sqrt(6) < z < -2
-2 < z < sqrt(2)-2
z<-2-sqrt(2)
Vamos a ponerlo como intervalos aproximados que si no no veremos nada
(2,45, +oo)
(-2,45, -2)
(-2, -0,59)
(-oo, -3,41)
Y puestos en orden son (-oo, -3,41)U(-2,45, -2)U(-2,-0,59)U(2,45,+oo)
Y con los números reales correctos es:
(-oo, -2-sqrt(2)) U (-sqrt(6), -2) U (-2, sqrt(2)-2)) U (sqrt(6),+oo)
No creas que tan seguro estoy de que no me haya equivocado, ahora mismo haré la gráfica para comprobarlo.
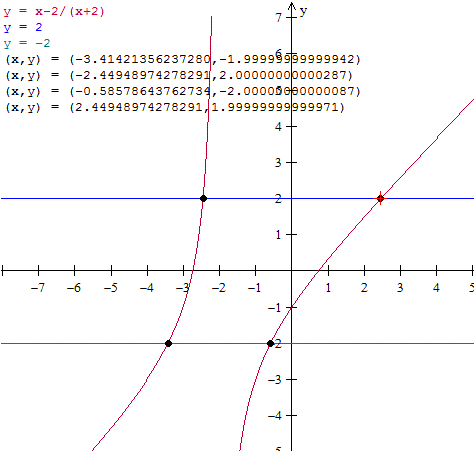
Y es justamente lo que había resuelto, luego está bien.
Y eso es todo.