Problema de geometría. Ayuda por favor!
Un deportista de
salto de longitud, logra un salto de 8 m de longitud, la
altura máxima alcanzada fue de 1.8 m. Describe las ecuaciones canónica y
general de la cónica que representan
dicho evento, elabora la gráfica correspondiente y elabora una tabla con
elementos correspondientes a la cónica resultante.
1 Respuesta
La curva que describe un objeto lanzado al aire hacia arriba con determinado angulo, velocidad inicial y sin tener en cuenta la fuerza de rozamiento del aire es una parábola.
Dicha parábola es simétrica respecto a la vertical que pasa por su vértice
Luego si salta en el punto (0,0) y cae en el punto (8,0) el vértice es
(4, 1.8)
Su ecuación general es
(x-4)^2=2p(y-1.8)
Para que pase por el punto (0,0)
(-4)^2 = 2p(0-1.8)
16 = - 3.6p
p = - 16/3.6 = -160/36 = -40/9 = -4.44444...
luego la ecuación canónica es
(x-4)^2 = - 2(40/9)(y-1.8)
prescindiendo del 2 del p sería
(x-4)^2 = -(80/9)(y-1.8)
Y la forma general es:
x^2 - 8x + 16 = -80y/9 + 16
9x^2 - 72x = - 80y
9x^2 - 72x + 80y = 0
El valor p es la distancia con dirección entre la directriz y el foco de tal modo que
el foco es vértice+ p/2 y la directriz pasa por centro - p/2
Foco = (4, 1.8) + (0, -40/18) = (4, -19/45)
Directriz pasa por (4, 1.8) - (0, -40/18) = (4, 181/45)
Es y = 181/45
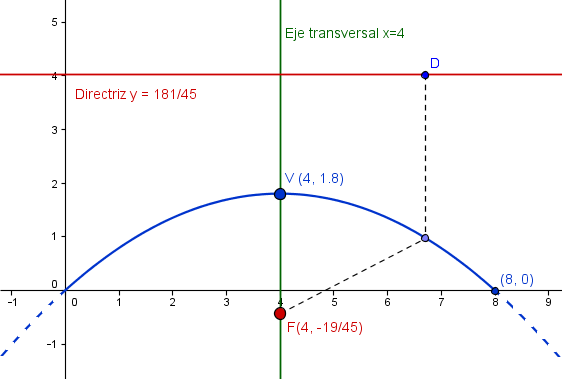
Esta es la tabla de datos de la cónica:
Ecuación canónica: (x-4)^2 = - 2(40/9)(y-1.8)
Ecuación general: 9x^2 - 72x + 80y = 0
Distancia directriz-foco, p: -40/9
Vértice: (4, 1.8)
Eje transversal: x=4
Foco: (4, -19/45)
Directriz: y = 181/45
Y eso es todo.
Hola amigo(a) Valeroasm!
Excelente respuesta, me ha servido muchísimo y le entendí perfecto tu explicación.
Agradezco infinitamente su atención y su apoyo desinteresado.
Saludos cordiales.
