Resuelve el problema utilizando la razón de cambio y tangente a una curva

Creo que querías decir

f(x) = (x-1) / (x+1)

En las fracciones hay que poner entre paréntesis los numeradores o numeradores que abarquen más de un termino

Ya que veo que usas el editor de ecuaciones escribe esto y la tendrás escrita en forma natural

f(x) = frac{x-1}{x+1}

La derivada de una fusión en un punto es la tangente del ángulo que forma la recta tangente con el semieje OX+.

Luego si nos dicen que ese ángulo es Pi/4 la tangente será

tg(Pi/4) = sen(pi/4) / cos(pi/4) = sen45º / cos45º = 1

Ya que sabemos que el seno y coseno de 45º son iguales

Luego la derivada es 1 en esos puntos, vamos a averiguar cuáles son

$$\begin{align}&f(x) = \frac{x-1}{x+1}\\ &\\ &f'(x) = \frac{x+1-x+1}{(x+1)^2}= \frac{2}{(x+1)^2}\\ &\\ &1=\frac{2}{(x+1)^2}\\ &\\ &(x+1)^2 = 2\\ &\\ &x+1= \pm \sqrt 2\\ &\\ &x=-1\pm \sqrt 2\\ &\\ &x_1=-1+ \sqrt 2\\ &x_2=-1-\sqrt 2\\ &\\ &f(x_1)=\frac{-2+ \sqrt 2}{\sqrt 2}=\frac{-2 \sqrt 2+2}{2}=1-\sqrt 2\\ &\\ &f(x_2)=\frac{-2-\sqrt 2}{-\sqrt 2}=\frac{2 \sqrt 2+2}{\sqrt 2}=1+\sqrt 2\\ &\\ &\\ &\text{La ecuación de la tangente en }(x_0,y_0)\; es\\ &\\ &y =y_0+f'(x_0)(x-x_0)\\ &\\ &\text{Luego en }(-1+ \sqrt 2,1- \sqrt 2)\; es\\ &\\ &y =1-\sqrt 2+1[x-(-1+\sqrt 2)]\\ &y =x+2-2 \sqrt 2\\ &\\ &\text{Y en }(-1- \sqrt 2,1+ \sqrt 2)\; es\\ &\\ &y =1+\sqrt 2+1[x-(-1-\sqrt 2)]\\ &y =x+2+2 \sqrt 2\\ &\end{align}$$

Hice la gráfica para asegurarme que esta ba bien

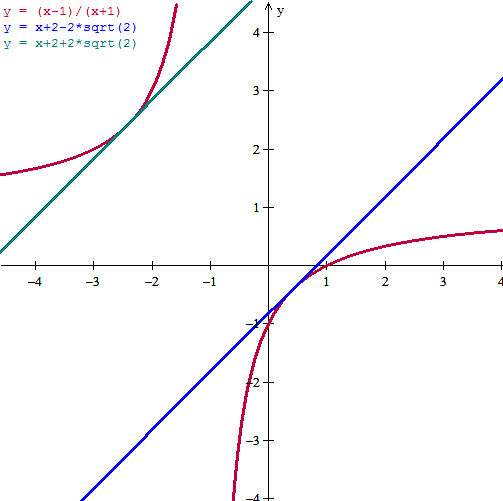
Y eso es todo.