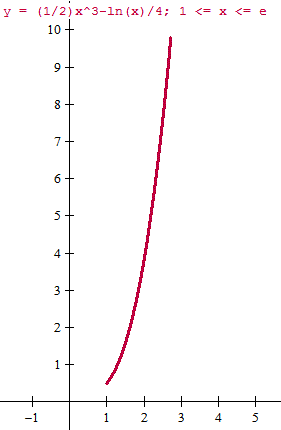Hallar la longitud de la curva entera o del arco indicado
y= (1/2)x^3 - (1/4)ln x desde x=1 a x=e
POR FAVOR necesito de su ayuda
1 respuesta
La longitud del arco es la integral de la raíz cuadrada de (1 + la derivada al cuadrado).
Y la función tiene que estar muy bien preparada ya que si no lo más fácil es que no se pueda resolver por el método de la función primitiva. En una figura tan sencilla como la elipse que no sea circunferencia no se puede calcular el arco. Pero veamos si esta se puede calcular.
$$\begin{align}&f(x) = \frac{x^3}{2}-\frac{lnx}{4}\\ &\\ &f'(x) = \frac {3x^2}{2}-\frac{1}{4x}= \frac{12x^3-2}{8x}=\frac{6x^3-1}{4x}\\ &\\ &\\ &l=\int_1^e \sqrt{1+\left( \frac{6x^3-1}{4x} \right)^2}dx=\\ &\\ &\\ &\int_1^e\sqrt{\frac{16x^2+36x^6-12x^3+1}{16x^2}}=\\ &\\ &\\ &\int_1^e\frac{\sqrt{16x^2+36x^6-12x^3+1}}{4x}=\end{align}$$Y como te decía, para poder calcular la integral de una raíz cuadrada lo de dentro debe estar medido al milímetro y en los casos más sencillos puede ser imposible, y en este más imposible aun.
Mira lo que dice el programa WolframAlpha
Que el resultado no se puede expresar en términos de funciones matemáticas estándar.
Luego la pregunta es de dónde ha salido este ejercicio y a qué se refiere el capítulo donde sale. Si se refiere a métodos de integración numérica aproximada se podrá hacer, pero me tendrías que pasar la teoría hay cien mil métodos para hacerlo.
Si el ejercicio no es de libro sino de tu cosecha ten en cuenta que las longitudes de arcos solo se pueden calcular por función primitiva un un número muy pequeño de ocasiones.
$$y = \frac{1}{2}x^3 - \frac{1}{4} ln x$$creo que no me di a entender soy nuevo y gracias por contestar el problema seria con el de arriba con los mismos valores de x (1 y e) aunque no se si aun se podría resolver
Si esa función es la que usé lo que pasa es que yo lo puse en la forma
(numerador x algo)/denominador
en vez de
(numerador/denominador) x algo
Y ya vimos que por el método habitual no se puede hacer
En la otra pregunta te he dado la respuesta realizado por ordenador con métodos numéricos.
9.509664135013573
Y en este momento no podría hacerte yo un método de rectángulos, trapecios, Simpson o similar porque el ordenador donde tengo los lenguajes de programación no arranca.
Muchas gracias, en realidad no viene mucha información el problema nos los dio el maestro
solo tiene como tema principal longitud del arco también viene la solución o repuesta del problema que seria
$$\frac{1}{2}e^3 - \frac{1}{4} unidades$$
el problema radicaría en como hacer el procedimiento para llegar a ese resultado
(1/2) e^3 - 1/4 = 9.7927768462
Contra la respuesta exacta que es
9.509664135013573
Pues no se puede decir que se hayan lucido mucho con la respuesta. No se como la habrán calculado porque puede haber cientos de truquillos, pero el que hayan empleado es muy malo.
Esta es la gráfica
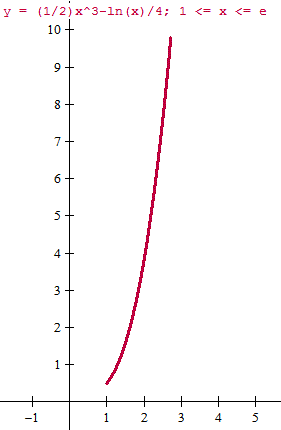
Lo que más llama la atención es que se hayan pasado de largo porque la función es siempre cóncava (o convexa según otros) y tomando segmentos ente puntos de la gráfica su suma será siempre menor a la real.
Simplemente si tomamos en punto inicial y final tenemos
(1, 1/2) a (e, e^3/8 - 1/4)
sqrt[(e-1)^2 +(e^3/2-3/4)^2] = 9.450293018
Que ya es una aproximación mejor que la respuesta que te dan.
Si tomas un punto intermedio en =2 y sumas los dos segmentos te da
sqrt[(2-1)^2+(f(2)-f(1))^2] + sqrt[(e-2)^2+(f(e)-f(2))^2]
9.482900140884613
Hacíendolo con puntos en x=1, 1.5, 2 y e tenemos este resultado
9.500524190699164
Y si lo hiciésemos con más puntos intermedios llegaríamos a la respuesta que da Máxima o WolframAlpha.
Luego es incomprensible de donde han podido sacar esa respuesta tan mala.
Y eso es todo.
