Problemas de análisis y predicción. 1

Amo 1965!

Supongo que tendrás los apuntes de la Universidad Abierta y a Distancia de Méjico sobre este tema que son

Procesos estocáticos. Unidad2. Cadenas de Markov a tiempo discreto.

Sin ellos a lo mejor no entiendes lo que hago, si no los tienes házmelo saber y veremos como te los puedo proporcionar.

Se supone que habrá que usar el teorema fundamental de la convergencia, para lo cual habría que ver que se cumplen las condiciones de que sea aperiódica, irreducible y recurrente.
Los estados que pueden estar los libros son 6
1) 123
2) 132
3) 213
4) 231
5) 312
6) 321
El libro que se quita pasa a primer lugar y los otros dos guardan su posición relativa,
Asi por ejemplo si tenemos 123
Si quitamos el 1 se va 123
Si quitamos el 2 se va a 213
Si quitamos el 3 se va a 312
Las probabilidades de paso son
1/3 0 1/3 0 1/3 0
0 1/3 1/3 0 1/3 0
1/3 0 1/3 0 0 1/3
1/3 0 0 1/3 0 1/3
0 1/3 0 1/3 1/3 0
0 1/3 0 1/3 0 1/3
Podemos comprobar que tenemos este ciclo de las permutaciones de 6 elementos
(1,3,6,2,5,4)
Luego todos los estados están comunicados y hay una única clase de comunicación y es irreducible.
Por el ciclo que hemos puesto arriba es posible llegar de cualquier estado a sí mismo en 6 pasos
Voy a poner el dibujo para ver si se puede llegar en otra cantidad de pasos

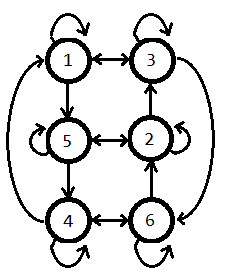
1--->3--->1
2--->5--->2
....
siempre se puede volver en 2 pasos
1--->5--->4--->1
2--->3--->6--->2
3--->6--->2--->3
4--->1--->5--->4
5--->4--->1--->3
6--->2--->3--->6
Y también se puede volver en 3
Luego el periodo es mcd(2,3)=1 y es aperiódica.
Y es recurrente por ser irreducible.
Luego se puede aplicar el teorema que dice

$$\begin{align}&a)\lim_{n\to oo} p_n(j,j) = \frac{1}{\mu_j}\\ &\\ &b)\lim_{n\to oo} p_n(i,j) = \frac{1}{\mu_j}\end{align}$$

Veamos cuál es el valor de mu sub jota.
La proposición 6 dice que una cadena de Markov irreducible y recurrente positiva tienen una
única distribución invariante cuyo elemento j-esimo es 1/(mu sub jota), luego si encontramos la cadena invariante encontraremos 1/(mu sub jota) que es el límite.
Solo espera que vea qué es eso de recurrente positiva, recurrente sé que lo es, pero positiva no sé que significa. Bueno, en los apuntes no lo he encontrado pero en otro sitio
he visto un teorema que dice que si el número de estados es finito entonces un suceso recurrente es recurrente positivo, luego la esta cadena es recurrente positiva.
Y se me antoja que la distribución invariante tiene que ser (1/6,1/6,1/6,1/6,1/6,1/6) porque no veo nada que haga a un estado distinto de los demás. Asi que en vez de resolver la ecuación voy a comprobar que esa distribución la verifica
Sea V=(x1, x2, x3, x4, x5, x6) la distribución invariante, debe cumplirse
V·P = V
eso se traduce en ecuaciones
(1/3)x1 + (1/3)x3 + (1/3)x4 = x1
(1/3)x2 + (1/3)x5 + (1/3)x6 = x2
.....
Puede verse que todas tienen tres coeficientes (1/3) y la variable de la derecha está siempre en la izquierda
Luego se traduce en 6 ecuaciones del tipo
-(2/3)xi + (1/3) xj + (1/3)xk = 0
que el verificarlas con (1/6,1/6,1/6,1/6,1/6,1/6) se cumple
-(2/3)(1/6) + (1/3)(1/6) + (1/3)(1/6) = 0
Luego esa distribución es invariante y la suma de los 6 términos es 1, luego es la solución única, luego
1/(mu sub j) = 1/6
Y por el teorema fundamental el límite es pn cuando n -->oo es 1/6

Y eso es todo.