Resolución de Cónicas

Esta vez me aseguro cual es el eje longitudinal para no tener que rectificar después de hecho todo. Focos y vértices están a altura 2, luego el eje longitudinal es la recta y=2 que es horizontal y es la manera más habitual de representación.

Vemos que el vértice no está entre los focos, luego es una elipse.

El centro es el punto medio de los focos

(h, k) = (1/2)[(1, 2)+(9, 2)] = (1/2)(10, 4) = (5, 2)

La ecuación canónica es

(x-h)^2 / a^2 + (y-k)^2 / b^2 = 1

a es el semieje positivo, la distancia del centro a los vértices del eje X

a = 11-5 = 6

Lego tenemos c que es la semidistancia focal, la distancia del centro a los focos.

c =9-5 = 4

Y el semieje menor b se calcula dado que

a^2=b^2 + c^2

b^2 = a^2 - c^2 = 6^2 - 4^2 = 36-16 = 20

Yen realidad con b^2=20 es suficiente porque es lo tenemos que usar en la fórmula

(x-5)^2/36 + (y-2)^2/20 = 1

Para obtener la general

5(x-5)^2 + 9(y-2)^2 = 180

5x^2 + 9y^2 - 50x - 36y +125 + 36 = 180

5x^2 + 9y^2 - 50x - 36y -19 = 0

Y esta es la gráfica hecha con Geogebra

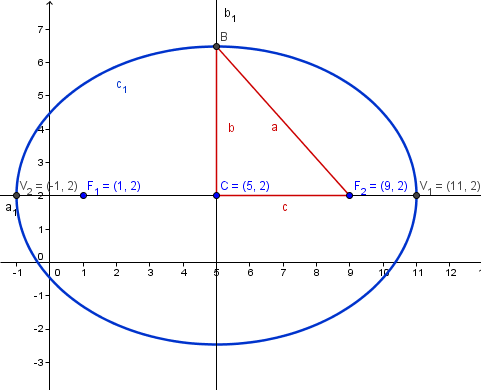
Y eso es todo.