Necesito ayuda para resolver tres cónicas.

Es importante saber el tipo de cónica si el resto de datos no es suficiente

1) Siendo una parábola el eje es la linea que une el foco y el vértice

Los puntos (2,3) y 5,3 están en la recta y=3 que es paralela al eje x

Las parábolas con eje paralelo al eje x tienen la siguiente ecuación canónica

(y-k)^2 = 2p(x-h)

Donde (h, k) es el centro y p es la distancia (con signo) entre directriz y foco

Esto hay que entenderlo bien.

Si la directriz está a la izquierda del foco (forma de C) p tiene signo positivo y si la directriz está a la derecha del foco tiene signo negativo.

Sabemos que la distancia directriz al vértice es igual a la distancia vértice al foco.

En este caso el vértice está a la izquierda del foco, y la directriz está a esa misma distancia a la izquierda del vértice, luego la directriz está a la izquierda del foco y p tendrá el signo +. Y su valor es el doble de la distancia vértice-foco.

Distancia vértice-foco = 5-2=3

p = 2·3 = 6

Luego la ecuación canónica es

(y-3)^2 = 2·6·(x-2)

que podemos poner de otra forma si queremos

y^2 - 6y +9 = 12x -24

y^2 - 12x - 6y + 33 = 0

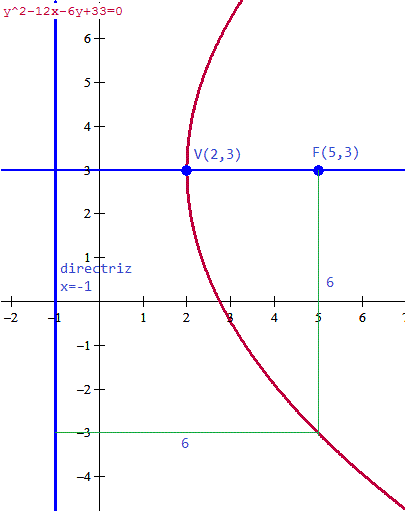
Y la gráfica es esta

Si quieres los otros ejercicios manda cada uno en una pregunta propia