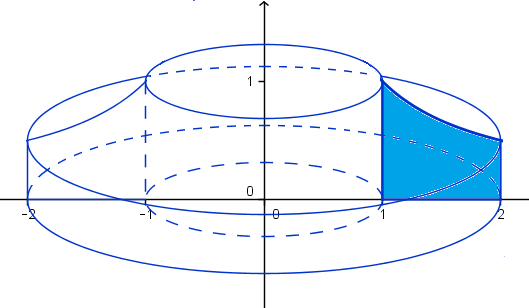
Halla el volumen generado al girar la región acotada
Halla el volumen generado al girar la región acotada por las curvas dadas alrededor del eje y.
a) y=1/x, y=0, x=1, x=2
Me piden realice un bosquejo de la regíón calculada, tengo el resultado pero parece algunos los he sacado mal, mi resultado es:
$$\int^2_1\frac{2nx}{x}dx=2 \pi$$Si es que está bien solo me faltaría el bosquejo, muchas gracias.
1 Respuesta
Por girar alrededor del eje Y debemos hacer la integral con la función x=f(y)
O sea x= 1/y
Cuando x=1 se tiene y=1
Cuando x=2 se tiene y=0.5
Luego los límites en y son 0.5 y 1
Este es el dibujo que confirma todo eso
Y el volumen se calcula así. Primero calculamos el volumen de la pieza maciza. Hasta y=0.5 es un cilindro, entre 0.5 y 1 es la función que habrá que integrar. Y a eso se le resta el hueco que es un cilindro entre y=0 e y=1
Volumen cilindro exterior entre 0 y 0.5 = pi·2^2·0.5 = 2pi
Volumen cilindro interior entre 0 y 1 = pi·1^2·1 = pi
Volumen macizo de la función entre 0.5 y 1
$$\begin{align}&\pi\int_a^b[f(y)]^2 dy =\\ &\\ &\\ &\pi\int_{0.5}^1 \frac{dy}{y^2}= \pi \left[-\frac 1y \right]_{0.5}^1=\pi(-1+2)=\pi\\ &\\ &\end{align}$$Luego el volumen de la pieza es
2pi+pi-pi = 2pi
Y eso es todo.
