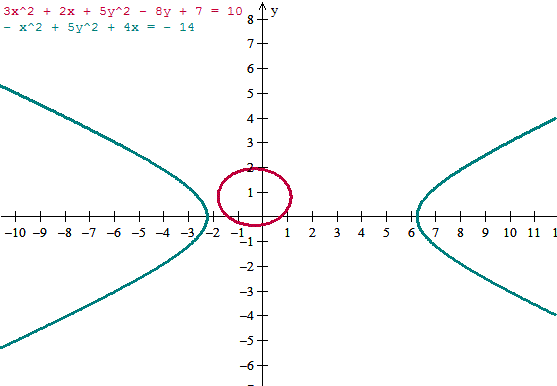Ecuaciones de segundo grado (12)

Esta es más complicada, haremos primero la gráfica.

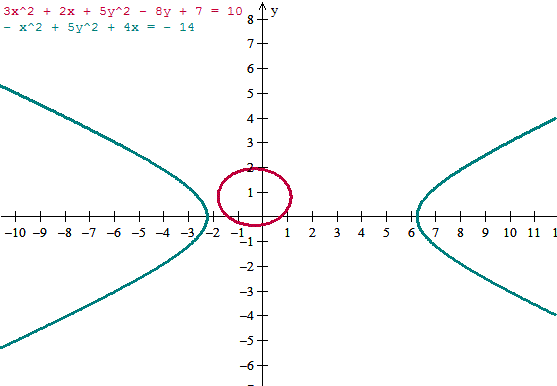
Bueno, ya sabemos que no se cortan. Vamos a demostrarlo analíticamente.

Anoche intenté hacerlo buscando las soluciones de las ecuaciones y salió algo inmanejable.

Vamos a hacerlo demostrando que la elipse tiene un dominio que la hipérbola no lo tiene, con lo cual no pueden tener puntos comunes.

La elipse es

3x^2 + 2x + 5y^2 - 8y + 7 = 10

3x^2 + 2x +5y^2 - 8y - 3 = 0

despejamos x

$$\begin{align}&x=\frac{-2\pm \sqrt{4-60y^2+96y+36}}{6}=\\ &\\ &\frac{-1\pm \sqrt{-15y^2+24y+10}}{3}\\ &\\ &\text{Veamos el máximo del discriminante}\\ &\\ &D´(y)=-30y+24 =0\\ &y = 24/30 = 4/5\\ &D(4/5) = -15·\frac{16}{25}+24·\frac 45+10 = 98/5\\ &\\ &\\ &x_{min}=\frac{-1-\sqrt{\frac{98}{5}}}{3}=-1.8090629\\ &\\ &x_{max}=\frac{-1+\sqrt{\frac{98}{5}}}{3}=1.142392241\\ &\\ &\end{align}$$

Esos son los valores de x para los vértices de la elipse.

Y ahora vamos a ver el dominio de la hipérbola

- x^2 + 5y^2 + 4x = - 14

x^2 - 4x - 5y^2 - 14 = 0

$$\begin{align}&x =\frac{4\pm \sqrt{16+20y^2+56}}{2}=\\ &\\ &2\pm \sqrt{18+5y^2}\\ &\\ &\text{El valor minimo del radicando es}\\ &\\ &\sqrt{18}=4.24264006687\\ &\\ &\text{con ello}\\ &\\ &x < 2-4.24264006687 \\ &x < -2.242640687\\ &\\ &\\ &x> 2 +4.24264006687\\ &x> 6.242640687\end{align}$$

Con lo cual se ve como el dominio de la elipse está metido dentro de la la zona donde no tiene dominio la hipérbola y por lo tanto es imposible que haya puntos comunes.

-2.2426... < -1.8090... < 1.1423... < 6.2426

Y eso es todo, ha sido un salto brutal el que se ha dado con este ejercicio respecto de los anteriores.