El volumen generado por la rotación del área entre la parábola y= 4x-x^2 con respecto a la recta

No sé si se verá bien en el gráfico. La figura tendrá un hueco central. Lo que tenemos que hacer es restar el volumen de ese hueco al volumen del cilindro.

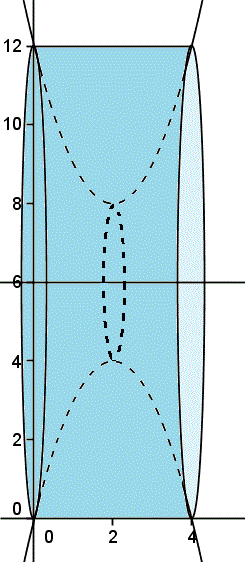
Si colocamos el nuevo eje X en la recta y = 6 la ecuación de la parábola se transforma en

y = 4x - x^2 - 6

Y el volumen que generará al girar, que es el volumen del hueco central será:

$$\begin{align}&V_{hueco}=\pi \int_0^4(4x-x^2-6)^2dx=\\ &\\ &\\ &\text{La fórmula del trinomio al cuadrado es:}\\ &(a+b+c)^2 = a^2+b^2+c^+2ab+2ac+2bc\\ &\\ &\\ &\\ &\pi \int_0^4(16x^2+x^4+36-8x^3-48x+12x^2)dx =\\ &\\ &\\ &\\ &\\ &\\ &\\ &\\ &\pi \left [  \frac{16x^3}{3} +\frac{x^5}{5}+36x-2x^4-24x^2+4x^3\right ]_0^4=\\ &\\ &\\ &\pi \left (\frac{1024}{3} +\frac{1024}{5}+144-512-384+256 \right )=\\ &\\ &\\ &\pi \left ( \frac{1024}{3} +\frac{1024}{5}-496  \right )=\\ &\\ &\\ &\\ &\pi \left ( \frac{5120+3072-7440}{15} \right )= \frac{752 \pi}{15}\\ &\end{align}$$

Como decíamos ese el el volumen del hueco, mientras que el del cilindro es:

$$V_{cilindro}=\pi r^2h=\pi·6^2·4 =144 \pi$$

Y el volumen que nos piden es:

$$V=144 \pi - \frac{752 \pi}{15}=\frac{(2160-752)\pi}{15}=\frac{1408 \pi}{15}\approx 294,89083u^3$$

Y eso es todo.