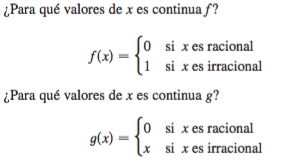·
·
¡Hola Lola!
f(x) no es continua en ningún punto, en cualquier entorno que tomes del número tendrás puntos donde la función valga 0 y otros donde valga 1, asi es imposible que todos disten una cantidad menor de épsilon de un límite fijo cuando epsilon sea menor de 1/2
·
g(x) es continua solo en el punto x=0 y en los demás discontinua
En el 0 basta tomar delta=epsilon y todos los puntos tales que
|x-0| < delta cumplirán |g(x) - g(0)| =|g(x)-0| < epsilon
·
62) Tendremos que ver que la función es continua en [-1, 1] o en algún intervalo contenido en él, o sea [a,b] con a>-1, b<1 y donde la función en los extremos tenga signos contrarios. Vemos inmediatamente que el primer denominador tiene una raíz para x=-1
Haciendo la división por Ruffini o por división entera de (x^3+2x^2-1) /(x+1) te queda x^2+x -1 cuyas raíces son
(-1-raíz(5))/2 = -1.6180339887
(-1+raiz(5))/2 = 0.618033989
Esta segunda raíz está dentro del intervalo [1,1] luego solo podemos garantizar la continuidad del primer término en
((-1+raiz(5))/2, infinito)
Veamos si el otro denominador da problemas, enseguida se ve que 1 es una raíz y al dividir por (x-1) queda x^2+x+2 que no tiene raíces, luego este no da problemas añadidos
Podemos decir que el segundo término es una función continua en
(-Infinito, 1)
Y entonces la suma de los dos términos es una función continua en
((-1+raiz(5))/2, 1)
Puesto que el valor en esos extremos tiende a infinito y la función es continua dentro se puede tomar un epsilon suficientemente pequeño tal que f sea continua en
[(-1+raiz(5))/2 + epsilon, 1-epsilon]
Y el signo de f[(-1+raiz(5))/2 + epsilon] sea el del infinito al que tiende la función en (-1+raiz(5))/2 por la derecha, y el signo de f(1-epsilon) sea el del infinito al que tiende f(1) por la izquierda
Con eso ya se podría usar el toerema de Bolzano, solo debemos verificar los signos del infinito de esos límites laterales y ver que son distintos.
$$\begin{align}&\lim_{x\to \left(\frac{-1+ \sqrt 5}{2}\right)^+}\frac{a}{x^3+2x^2-1}+\frac{b}{x^3+x-2}=\\&\\&\lim_{x\to \left( \frac{-1+ \sqrt 5}{2}\right)^+}\frac{a}{(x+1)\left(x-\frac{-1- \sqrt 5}{2} \right)\left(x-\frac{-1+\sqrt 5}{2} \right)}+\frac{b}{x^3+x-2}=\\&\\&\text{como } \frac{-1+ \sqrt 5}{2}=0.6180339887\text{ tendremos}\\&\\&x+1\to0.6180339887\gt 0\\&\\&x-\frac{-1-\sqrt 5}{2}\to \frac{-1+ \sqrt 5}{2}-\frac{-1-\sqrt 5}{2}=\sqrt 5\gt 0\\&\\&x-\frac{-1+ \sqrt 5}{2}\gt 0 \quad\text {por ser límite lateral derecho}\\&\\&a\gt 0 \text{ por hipótesis}\\&\\&\text{Los cuatro factores son positivos, luego el límite será}\\&\\&\lim_{x\to \left(\frac{-1+ \sqrt 5}{2}\right)^+}f(x) =+\infty+ (cantidad finita)=+\infty\\&\\&·\\&\\&\text{Y el límite izquierdo en x=1 es}\\&\\&\lim_{x\to 1^-}{}\frac{a}{x^3+2x^2-1}+\frac{b}{x^3+x-2}=\\&\\&\lim_{x\to 1^-}{}\frac{a}{x^3+2x^2-1}+\frac{b}{(x-1)(x^2+x+2)}=\\&\\&x-1\lt0 \quad\text{ya que }x\lt 1\\&\\&x^2+x+2 \to4\gt 0\\&\\&b\gt 0\\&\\&\text{Dos positivos y un negativo me da negativo y el límite es}\\&\\&=(un valor finito) - \infty = -\infty\\&\\&\text{Luego como decía, hay un intervalo (en realidad infinitos)}\\&\\&\left[\frac{-1+\sqrt 5}{2}+\epsilon\,,\quad 1-\epsilon \right]\\&\\&\text{donde la función es continua y los valores de los}\\&\text{extremos son opuestos}\\&\text{Luego por el teorema de Bolzano hay una raíz en}\\&\text{ese intervalo, que como está contenido en [-1, 1]}\\&\text{hace que la raíz esté contenida en[-1, 1]}\end{align}$$Y eso es todo, sa lu dos.
:
: