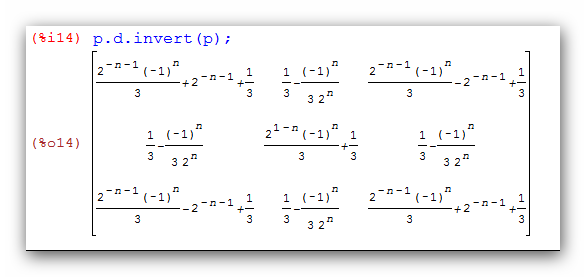Ejercicio sobre cadenas de markov
hola valeroasm! Tengo el siguiente ejercicio sobre cadenas de markov en donde hay que aplicar valores y vectores característicos. No tengo mucho conocimiento acerca del tema de cadenas de markov asi que quisiera que fueras lo mas claro y explicito conmigo para solucionar el siguiente ejercicio. Te lo agradezco desde ya.
1 Respuesta
No conocía este tema, así que me faltará precisión.
Un camión puede tener tres estados
B estar en Boston
C estar en Chicago
A estar en Los Ángeles
La probabilidad de estar el mes siguiente en un sitio solo depende del sitio donde está el mes anterior. Por eso es un proceso estocástico que se llama cadena de Markow.
Debemos hallar las probabilidades de transición de un estado a otro o a sí mismo y con esto se forma una matriz
P(B, B) = 1/2 Ya que la mitad de los camiones de Boston se quedan en Boston
P(B, C) = 1/2 Ya que a Chicago van la mitad de los de Boston
P(B, A) = 0 De Boston a Los Ángeles no van camiones
Estos tres datos forman la primera fila
La segunda sería la probabilidad de los camiones de Chicago
P(C,B)=1/2 P(C,C)=0 P(C,A)=1/2
Y la tercera de los camiones de Los Angeles
P(A,B)=0 P(A,C)=1/2 P(AA)=1/2
Queda esta matriz
| 1/2 1/2 0 |
A = | 1/2 0 1/2 |
| 0 1/2 1/2 |Creo que quedaría mejor con 0.5 pero en Matemática Superior los decimales están mal vistos.
El estado probable el mes siguiente de una cantidad X0^t = (x0, y0, z0) de camiones se obtiene mediante el producto matricial X0^t·A
El ^t significa transpuesto, ya que un vector se considera "bien puesto" cuando esta en columna
| 1/2 1/2 0 |
(x0, y0, z0) x | 1/2 0 1/2 | =
| 0 1/2 1/2 |(1/2)(x0+y0, x0+z0, y0+z0)
Esa es la distribución de camiones dentro de un mes.
Para el segundo mes habría que multiplicar el vector que nos ha dado por la matriz de nuevo
Segundo mes = (X0^t ·A)· A = X0^t · A^2
Y en general el el mes i-esimo será
i-ésimo mes = X0^t · A^i
No sé cuán fácil va a ser expresar esto, aplicaré la fórmula a la fórmula, porque no hay nada más horrible que escribir aquí multiplicaciones de matrices.
segundo mes = (1/4)(2x0+y0+z0, x0+2y0+z0, x0+y0+2z0)
tercer mes = (1/8) (3x0+3y0+2z0, 3x0+2y0+3z0, 2x0+3y0+3z0)
cuarto mes = (1/16)(6x0+5y0+5z0, 5x0+6y0+5z0, 5x0+5y0+6z0)
quinto mes = (1/32) (11x0+11y0+10z0, 11x0+10y0+11y0, 10x0+11y0+11z0)
Y esto es cuanto se puede obtener con este método rudimentario. El método bueno sería multiplicando matrices. Y el método óptimo para multiplicar matrices es diagonalizando la matriz. Para ello calculamos los valores propios. Ahora si va a ser un determinante
| 1/2-x 1/2 0 | | 1/2 0-x 1/2 | = 0 | 0 1/2 1/2-x |
-x(1/2-x)(1/2-x) -(1/2)(1/2-x) =
(1/2-x) (-x/2 + x^2 -1/2)
Un valor propio es 1/2
Calculamos los otros resolviendo x^2 - x/2 - 1/2 = 0
x= [1/2 +- sqrt(1/4 +2)]/2 =
[1/2+- sqrt(9/4)]/2 =
(1/2 +- 3/2) / 2 = 1 y -1/2
Luego los valores propios son
-1/2, 1/2, 1
Calculamos los vectores propios.
Para -1/2
1 1/2 0 1 1/2 0 1/2 1/2 1/2 ~ 0 1/4 1/2 0 1/2 1 0 1/2 1
Tomamos z=1 ==> y = -2 ==> x =1
vector de (-1/2) = (1, -2, 1)
Para 1/2
0 1/2 0 1/2 1/2 1/2 0 1/2 0
Tomamos z=-1 ==> x=1
y=0
vector de (1/2) = (1,0,-1)
Para 1
-1/2 1/2 0 -1/2 1/2 0 1/2 -1 1/2 ~ 0 -1/2 1/2 0 1/2 -1/2 0 0 0
tomamos z= 1 ==> y=1 ==> z=1
Luego el vector propio es (1,1,1)
La matriz de paso (P), la diagonalizada(D) y la inversa de la de paso (P^-1, cuyo cálculo omitiré) son
1 1 1 -1/2 0 0 1/6 -1/3 1/6 -2 0 1 0 1/2 0 1/2 0 -1/2 1 -1 1 0 0 1 1/3 1/3 1/3
Sabemos y se puede comprobar y lo he comprobado que
P^-1 · A · P = D
A = PDP^(-1)
A^n = [PDP^(-1)]^n = PDP^(1)PDP^(-1)....DP^(-1) = P D^n P^(-1)
Con esto tendremos
| 1 1 1| |(-1/2)^n 0 0| |1/6 -1/3 1/6|
A^n = |-2 0 1| x| 0 (1/2)^n 0| x |1/2 0 -1/2|
| 1 -1 1| | 0 0 1| |1/3 1/3 1/3|Bueno, si quieres multiplicas las matrices, es tedioso hacerlo y escribirlo aquí también.
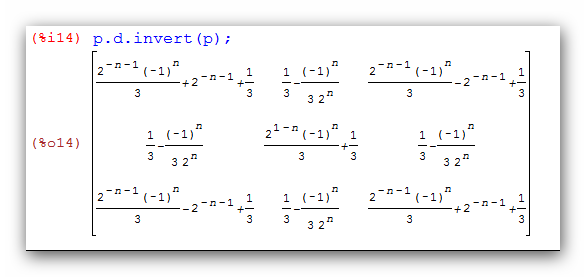
Esto es lo que me ha dado el programa Máxima.
Como puede verse, todos los elementos de la matriz tienen una parte que es 1/3 y luego unas funciones de n. Unas veces sirven para determinar el signo y otras para aportar valor, pero fíjate que en todas estas el exponente de n es negativo o bien es positivo pero está en el denominador. Eso significa que cuando n tienda a infinito esas funciones de n tenderán a cero y quedará una matriz toda llena de 1/3
Y cuando multipliquemos el vector de camiones iniacales por esta matriz, el límite en el mes infinito va a ser
1/3(x0+y0+z0, x0+y0+z0, x0+y0+z0)
Es decir que los camiones acabarán repartiéndose por igual entre las tres sedes.
Y eso es todo, espero que te sirva y lo hayas entendido. No más problemas de estos por favor, a no ser que vayan acompañados con varios triviales que compensen el esfuerzo.
