Si hacés el ejercicio para distintos valores de 'a', vas a ver que la primer expresión es una circunferencia donde si a es positivo estará a la derecha del eje 'Y', mientras que si a es negativo la circunferencia estará a la izquierda de dicho eje. (El modulo de a determinará el tamaño de la circunferencia).
Te dejo una imagen de ejemplo, donde asumí que 'a' es + /- 4
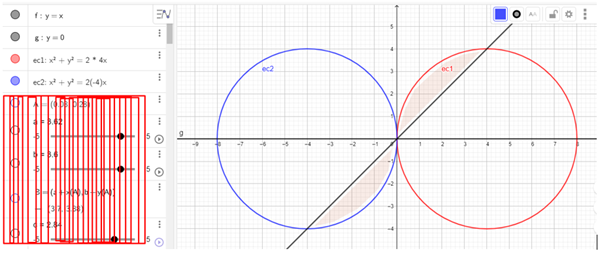
Lo que sombreé es el área que te están pidiendo. Como ves, para cualquiera de los dos valores de a posibles (positivos o negativos), el área es equivalente ya que es simétrica respecto al origen.
Dicho esto, podés asumir que 'a' será negativo y calcular el área de ese arco. Uno de los extremos será el origen y el otro estará dado por la intersección entre la circunferencia y la recta y=x. O sea
y=x
x^2+y^2 = 2ax
Reemplazo la primera en la segunda
x^2+x^2 = 2ax
2x^2 = 2ax
x^2 = ax
x^2-ax = 0
x (x-a) = 0
Las opciones son
x=0 (ya lo sabíamos)
x=a
O sea que lo que debemos calcular es la integral, entre 0 y a de la circunferencia menos la recta y=x
Acomodamos la expresión de la circunferencia
y = sqrt( -x^2 + 2ax)
O sea que el área será
$$\begin{align}&A = \int_0^a (\sqrt{-x^2+2ax}-x )dx\end{align}$$Te queda calcular esa integral...

