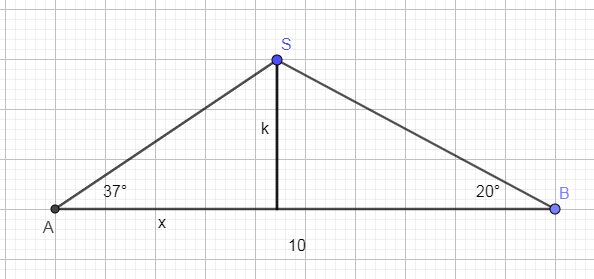
Dos puestos de observación, A y B (separados 10 millas) en la costa, vigilan barcos que entran ilegalmente en un
¿Ley del seno?
Dos puestos de observación, A y B (separados 10 millas) en la costa, vigilan barcos que entran ilegalmente en un límite de 3 millas. El puesto A reporta un barco ES en un ángulo BAS=37° y el puesto B reporta el mismo barco en un ángulo ABS = 20°. ¿A qué distancia está el barco del puesto A? ¿A qué distancia está el barco del puesto B? ¿A qué distancia está el barco de la costa?
Necesito
1 respuesta
En estos casos lo mejor siempre es hacer un dibujo para intentar entender lo que están preguntando...
En este caso están preguntando la distancia del segmento AS, del segmento BS y de k
Veamos lo que sabemos o podemos usar...
$$\begin{align}&tan(37)=\frac{k}{x} \to k=x \cdot tan(37)\\&tan(20)=\frac{k}{10-x} \to k=(10-x)tan(20)\\&Igualación...\\&x tan(37)=(10-x)tan(20)\\&0.75x = 3.6-0.36x\\&1.11x = 3.6\\&x=3.6/1.11 = 3.24\\&k=x\cdot tan(37)=3.24 \cdot 0.75 = 2.43\\&sen(37)=\frac{k}{AS} \to AS=\frac{k}{sen(37)}=\frac{2.43}{0.60}=4.05\\&sen(20)=\frac{k}{BS} \to BS=\frac{k}{sen(20)}=\frac{2.43}{0.34}=7.15\end{align}$$Sé que no lo resolví usando la "ley del seno", pero la verdad que no me gusta aprender las cosas de memoria y más cuando se puede deducir a partir de fórmulas mucho más 'elementales' como la fórmula del seno y de la tangente.
Salu2