A con esta priblemática 1. Introducción. Lee atentamente para conocer la relación de la la aplicación del modelo de Thomas Mal
- Introducción. Lee atentamente para conocer la relación de la la aplicación del modelo de Thomas Malthus, economista inglés en 1798, y el uso de la anti derivada.
En esencia, la idea de este modelo matemático de Malthus es la hipótesis de que la tasa de crecimiento de la población sin freno de un país crece en forma proporcional y constante P(t), de ese país en cualquier momento (t en años). En otras palabras, mientras más personas haya en el momento t, habrá más personas en el futuro. En términos matemáticos, esta hipótesis se puede expresar:
Donde el símbolo ∝ (alfa) indica que ambas cantidades son proporcionales y k es esa constante de proporcionalidad. Este modelo no tiene en cuenta otros factores (por ejemplo, inmigración y emigración) que pueden influir en las poblaciones humanas, haciéndolas crecer o disminuir, pero predijo con mucha exactitud la población de Estados Unidos desde 1790 hasta 1860. La ecuación diferencial anterior aún se utiliza con mucha frecuencia para modelar poblaciones de bacterias y de animales pequeños durante cortos intervalos.
Como se mencionó una de las aplicaciones principales de la anti derivada es la solución de ecuaciones diferenciales, si nos planteamos la ecuación anterior P' (t) = kP (t) podemos ponerla en la forma de diferencial, teniendo la ecuación:
dP = kP (t) dt
Ahora como la P es la variable dependiente podemos pensarla como solo y = P(t), de esta manera dP = dy y acomodando la ecuación anterior en términos de y nos resulta:
dy = kydt
Tenemos una igualdad entre dos diferenciales, para que cada lado tenga las mismas variables pasamos la y del lado derecho al lado izquierdo:
En este punto la ecuación está en forma de diferenciales y cada uno de los lados de la igualdad está en términos de una sola variable, para obtener las respectivas funciones que tienen esos diferenciales es necesario obtener su anti derivada. Integra las funciones en cada lado de la igualdad para hallar la solución de la ecuación diferencial, No olvides que cada función tiene su propia constante de integración:
Una vez que tengas las respectivas anti derivadas en la identidad despeja la variable y para que sea una función en términos de t, debes recordar las propiedades de las funciones necesarias. Tu proceso debe conducir a esta ecuación que es el modelo de Malthus:
y=ce^kt
Donde la variable y representa la tasa de crecimiento de la población.
- Desarrollo. Con la aplicación de la anti derivada del modelo de Malthus, sigue el planteamiento y resuelve lo que se indica:
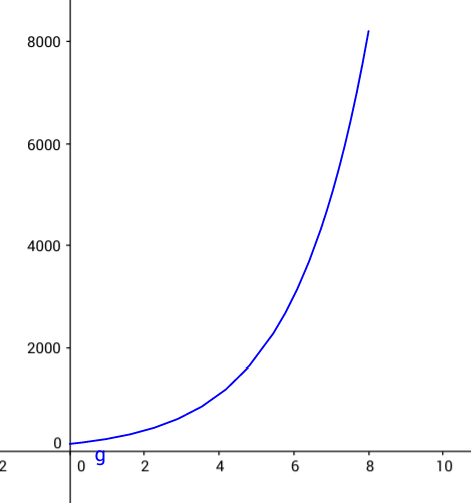
Suponiendo que la población inicial que se está considerando es de 180 individuos determina el valor de C. Si tenemos que k=0.5, y con la ecuación se estima el tamaño de la población dentro de 8 años. Bosqueja una gráfica a mano.
1 Respuesta
Con los datos el enunciado tenemos que para el tiempo inicial la población es 180 individuos, siendo "y" el número de individuos y "t" el tiempo, tendríamos:
$$\begin{align}&y=C\cdot e^{k\cdot t} \Rightarrow 150=C\cdot e^{k\cdot 0} \Rightarrow 150=C\cdot e^{0}\\\\&C=150\end{align}$$Por tanto, el valor de C es 150.
Para la segunda parte del problema, tenemos k=0.5 y t=8 años. Aplicando la ecuación tendríamos una población de:
$$\begin{align}&y=150 \cdot e^{0,5 \cdot 8}\approx8190\;individuos\end{align}$$Teniendo en cuenta que la gráfica es una exponencial y que la población inicial es de 180 individuos, la gráfica sería:
