Dominio de la funciòn log(1-2cosx)

;)
Hola candy maritza!

Cosx < 1/2 , no dará negativo, ya que ese coseno en el argumento del logaritmo está restando

(1-2cosx)

Igualmente no está acabado, eso es una inecuación trigonométrica que se ha de resolver.

Es decir calcular los ángulos (x) cuyo coseno es inferior a 1/2.

Esto como mejor se ve es gráficamente:(con la función coseno)

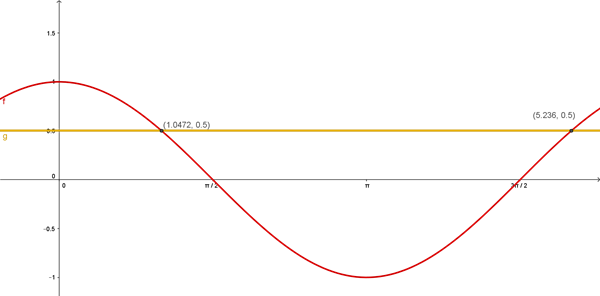
En amarillo la recta  y=1/2

Los puntos de corte son los ángulos cuyo coseno vale 1/2, que de forma exacta son pi/3 (60º) y 5 pi/3 (300º). Como queremos los ángulos con cos <1/2, el dominio queda:

$$\begin{align}&Domf(x)=( \frac{\pi}{3},\frac{5 \pi}{3})\\&\\&\frac{\pi}{3} < x < \frac{5 \pi}{3}\end{align}$$

en radianes.

Saludos

;)

;)