Como diferenciar con derivadas o limites los máximos y mínimos absolutos de los relativos.

;)
Hola Juana!

Los máximos y mínimos absolutos son los puntos donde la función (y) vale más y menos, respectivamente, en su Dominio.

Los máximos y mínimos relativos son los puntos donde la función vale más y menos, pero en una zona próxima(relativo). Por ello han de tener recta tangente horizontal (pendiente 0), porque a la izquierda y a la derecha del extremo relativo el crecimiento ha de cambiar.

Los máximos y mínimos absolutos pueden coincidir con los relativos; pero tiene por quë.

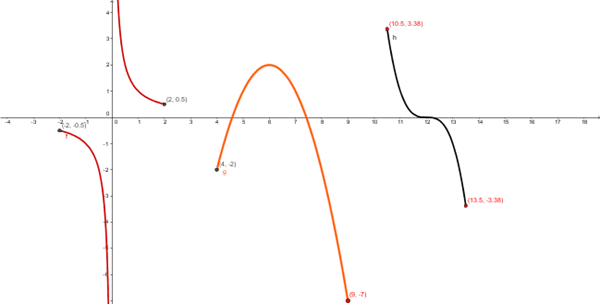
Mira la gráfica del medio: el máximo relativo también es el máximo absoluto(el vértice de la parábola). Ahora el mínimo sería el punto de la derecha. Esa parábola solo está definida de 4, a 9. f(9)=-7 es el menor absoluto.

Si una función es continua en un intervalo, los max y min absolutos, o bien coinciden con los relativos o bien se encuentran en los extremos del Dominio (en exte caso x=9). Por eso

Para calcular los max y min absolutos:

1º calcular  y'=0   ===> x=a  y calcular  f(a)

2º Calcular las imágenes en los extremos del Dominio.

Donde f(x) es mayor ==> mas abs

f(x)   menor  ==>min abs.

Observa la gráfica roja: Dom=[-1,1] No tiene extremos relativos: no hayrecta tangente horizontal.

Por otro lado tampoco tiene max y min absolutos , ya que

$$\begin{align}&\lim_{x\to 0^-}f(x)=- \infty\\&\\&\lim_{x\to 0^+}f(x)=+ \infty\end{align}$$

El  -infinito hace que no haya un óptimo mínimo

El + infinito hace que no haya un óptimo máximo.

Observa ahora la función de la derecha:Dom=[10.5, 13.5]

No tiene max ni min relativos.

MinAbsoluto en 13.5  f(13.5)=-3.38

Max Absoluto en x=10.5  f(10.5)=+3.38

En los problemas de optimización, la mayoría de veces el max y min absolutos coinciden con los relativos; pero ya verás que no siempre, y entoces hay que estudiar que pasa en los extremos del Dominio de Definición

Saludos

;)

;;