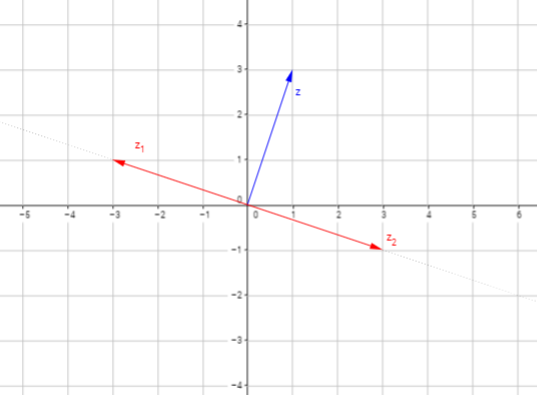
Cómo calcular el número complejo perpendicular al número (1+3i)
Como calcular giros de 90, 180 y 270 grados de un número complejo
2 respuestas
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1