Representar gráficamente los resultados de raíz cúbica de (-2-2i) y calcular el lado y el área del polígono que se obtiene
Áreas de polígonos que se obtienen de una raíz cúbica de un número complejo, tanto su lado como su área, de las figuras así obtenidas
1 Respuesta
$$\begin{align}& \end{align}$$Sabemos que la raíz enésima de un complejo cumple que:
$$\begin{align}&\text{Sea el complejo z = a+bi; r raíz enésima de z, entonces:}\\&Módulo:\\&|r| = \sqrt[n]{r}\\&Argumento:\\&a_r = \frac{a_z + 2k \pi}{n}.........k=0, 1, 2, ..., n-1 \text{ (en radianes) ó}\\&a_r = \frac{a_z + 360° k}{n}.........k=0, 1, 2, ..., n-1 \\&En\ este\ caso:\\&z=-2-2i\\&a_z = arctg\bigg(\frac{-2}{-2} \bigg) = 225°\\&|r| = \sqrt[3]{(-2)^2+(-2)^2} = \sqrt[3]{8} = 2\\&a_r = \frac{225° + 360° k }{3}.........k=0, 1, 2\\&a_{r1} = \frac{225° }{3} = 75°\\&a_{r2} = \frac{225°+360° }{3} = 195°\\&a_{r3} = \frac{225° + 360° \cdot 2}{3} = 315°\end{align}$$Claramente una raíz cúbica definirá un triángulo, y además será regular por lo que se trata de un triángulo equilátero.
Antes de hacer los otros cálculos que pide, veamos una imagen de las raíces en cuestión:
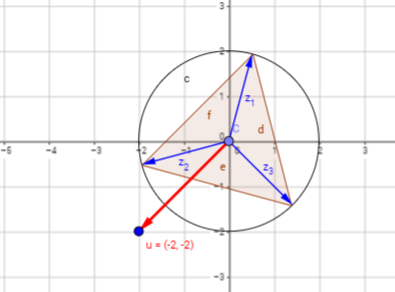
Sabemos que el lado medirá la distancia entre 2 cualesquiera de sus raíces, tomemos la raíz z1, z2, tenemos que:
$$\begin{align}&z_1 = (2 \cos(75°), 2 sen(75°))\\&z_2 = (2 \cos(195°), 2 sen(195°))\\&d(z_1,z_2) = \sqrt{(2cos(75°)-2cos(195°))^2+(2sen(75°)-2sen(195°))^2} = \\&2 \sqrt{(\cos(75°)-\cos(195°))^2+(sen(75°)-sen(195°))^2} = 2 \cdot \sqrt{3} \text{ (esto es lo que miden sus lados)}\\&\text{De la trigonometría, sabemos además que la altura de un triángulo equilatero de lado L es}\\&h = L \cdot sen 60° = L\cdot \frac{\sqrt 3}{2},\\&\text{En este caso}\\&h = 2 \sqrt{3} \cdot \frac{\sqrt 3}{2} = 3\\&\therefore\\&Area = \frac{L h}{2} = \frac{2 \sqrt{3} \cdot 3}{2} = 3 \sqrt{3}\end{align}$$
El módulo del complejo es raíz cuadrada de 8, que luego debemos hacer su raíz cúbica...luego los módulos de las tres soluciones no sería raíz de índice 6 de 8?
Uh... grueso error de mi parte y eso porque los números "quedaban lindos"
En base a eso voy a recalcular el área
$$\begin{align}&Primero\ veamos\ que:\\&\sqrt[6]{8} = 2^{3/6} = 2^{1/2} = \sqrt{2}\\&Ahora\ si,\ recalculo:\\&z_1 = \sqrt{2} (\cos(75°) + i sen( 75°))\\&z_2 = \sqrt{2} (\cos(195°) + i sen( 195°))\\&d(z_1,z_2) = \sqrt{(\sqrt 2 cos75°- \sqrt 2 \cos 195)^2 + (\sqrt 2 sen75°- \sqrt 2 sen 195)^2 }=\\&\sqrt{2} \sqrt{(cos75°- \cos 195)^2 + ( sen75°- sen 195)^2 }=\sqrt 2 \sqrt 3 = \sqrt{6}=L\\&h = \sqrt 6 \frac{\sqrt 3}{2}\\&Area = \frac{L h}{2} = \frac{1}{2} \sqrt{6} \frac{\sqrt 6 \sqrt 3}{2} = \frac{6 \sqrt 3 }{4} = \frac{3}{2} \sqrt 3\end{align}$$