Problema de calculo integral, integrales impropias

·

·

¡Hola Juan!

Supongo que estos son los primeros ejercicios que haces y no te van a poner algo problemático. Pero siempre hay que revisar que en el intervalo de integración la función no tiende a infinito en algún punto finito, ya que entonces se debería calcular la integral de el trozo derecho y el izquierdo por separado.

En esta el denominador se hace cero cuando

3x+1 = 0

x= -1/3

Vale, no entre en el intervalo de integración luego no hay problemas

$$\begin{align}&\int_0^{\infty}\frac{dx}{(3x+1)^2}=\lim_{R\to\infty}\int_0^R \frac{dx}{(3x+1)^2}=\\&\\&\text{Es medio directa, pero la haremos con cambio de}\\&\text{variable y así aprendes más. Sobre todo, fíjate que}\\&\text{yo cambio los límites a la vez que la variable, así}\\&\text{no tengo que hacer el descambio después.}\\&\\&t=3x+1\\&dt = 3dx\implies dx =\frac 13dt\\&x=0\implies t=3·0+1=1\\&x= R \implies t=3R+1=S\\&\\&\text{No vamos a hacer el tonto operando con 3R+1}\\&\text{pondremos una S que tiende igual a }\infty\\&\\&\lim_{S\to\infty}\frac 13\int_1^S \frac {dt}{t^2} =\frac 13\lim_{S\to \infty}\left[ -\frac 1t\right]_1^S=\\&\\&\frac 13 \lim_{S\to \infty} \left(-\frac 1S+\frac 11  \right)=\frac 13(0+1)=\frac 13\end{align}$$

Luego la integral es convergente y vale 1/3.

Sé que a lo mewjor no te haguastado el cambio de variable y menos el cambio simultáno de los límites de integración, por eso te lo hago haciendo la integral directamente.

$$\begin{align}&\int_0^{\infty}\frac{dx}{(3x+1)^2}=\lim_{R\to\infty}\int_0^R \frac{dx}{(3x+1)^2}=\\&\\&\lim_{R\to\infty} \frac 13·\frac {-1}{3x+1}\bigg|_0^{R}=\lim_{R\to \infty}\frac 13\left(\frac{-1}{3R+1}+\frac{1}{3·0+1}  \right)=\\&\\&\frac 13(0+1) =\frac 13\end{align}$$

Así es mucho menos pesado.

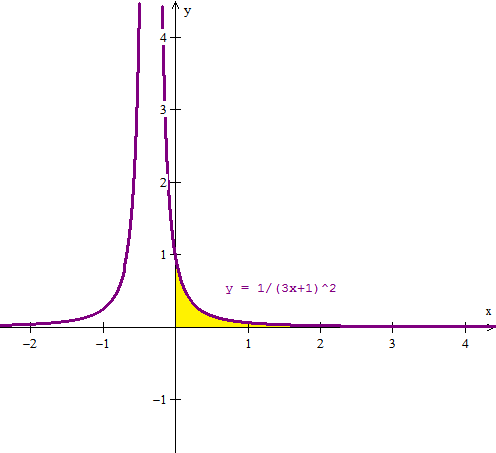
Y la grafica es esta.