Realizar siguiente la Integral definida
Obtener la integral definida del inciso presentado de bajo,
a)
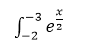
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Cristal!
$$\begin{align}&\int_{-2}^{-3}e^{\frac x2}dx=\\&\\&\text{Si derivaras } e^{\frac x2} \text{ te daría }\frac{1}{2}e^{\frac x2}\\&\text{luego para que te dé }e^{\frac x2}\\&\text{tienes que multiplicar por 2.}\\&\text{Así la derivada de }2e^{\frac x2}\; es\;e^{\frac x2}\\&\\&=2e^{\frac x2}\bigg|_{-2}^{-3}=2(e^{-\frac 32}-e^{-1})=\\&\\&2\left(\frac{1}{\sqrt {e^3}}-\frac 1e \right)=\frac 2e\left(\frac 1{\sqrt e}-1 \right)\end{align}$$Hay varias formas de dejarlo, a mí esa es la que más me gusta.
Saludos.
:
:
¡Gracias! ^¿podría ayudarme con esta por favor?
Realizar el siguiente ejercicio de integración para obtener la integral definida
Ya lo he hecho, lo estaba haciendo mientras mandabas la petición. NO olvides valorar todas las respuestas.
1 respuesta más de otro experto
Respuesta
1
Es una integral bastante inmediata, recordemos que
$$\begin{align}&(e^{ax})' = a\cdot e^{ax} \therefore\\&\int_{-2}^{-3}e^{\frac{x}{2}}=2\cdot e^{\frac{x}{2}}\bigg |_{-2}^{-3}=2\cdot \bigg(e^{\frac{-3}{2}} - e^{\frac{-2}{2}} \bigg)=\\&2\cdot \bigg(\frac{1}{e^{3/2}} - \frac{1}{e} \bigg)=2\cdot \bigg(\frac{1-e^{1/2}}{e^{3/2}} \bigg)\end{align}$$