Aplicación de los teoremas de trigonometría
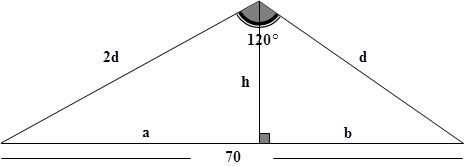
Una antena de telefonía móvil está sujeta al suelo con dos cables desde su punto más alto, y uno de los cables tiene doble longitud que el otro. Los puntos de sujeción de los cables al suelo están alineados con el pie de la antena, la distancia entre dichos anclajes es de 70 metros y el ángulo formado por los cables es de 120. Calcula la longitud de cada uno de los cables y la altura de la antena de telefonía.
2 Respuestas
Como estas Juana:
Del problema podemos obtener el siguiente gráfico:
El poste es el segmento vertical y los cables son las segmentos laterales:
Por la ley de cosenos:
Reemplazamos el valor del cos120° = - 1/2 y operamos
ñ
Por lo tanto:
Un cable medirá:
El otro cable medirá:
Para hallar la altura (h) (segmento vertical) aplicamos pitágoras a ambos triángulos rectángulos:
.......................(I)
.........................(II)
Restamos: I - II
Por diferencia de cuadrados:
Reemplazando: a + b = 70
Entonces: a - b = 30
Formamos un sistema de ecuaciones:
Resolvemos el sistema:
a = 50 ; b = 20
Reemplazamos en ecuación II:
Por lo tanto la altura del poste es:
e
Eso es todo, espero puedas entender. No te olvides de puntuar la respuesta y seguidme.
·
·
¡Hola Juana!
Podemos usar el teorema de los cosenos:
$$\begin{align}&\text{Sean a, b las longitudesde los cables}\\&\text{y sea c la longitud entre ellos en el suelo}\\&\\&c^2 = a^2 +b^2-2ab· cosC\\&\\&70^2 = a^2+b^2-2ab·\left(-\frac 12\right)\\&\\&\text{Suponiendo que a es el lado pequeño, }b=2a\\&\\&4900 = a^2 +4a^2 +2a^2\\&\\&7a^2=4900\\&\\&a^2=700\\&\\&a= \sqrt{700}=10 \sqrt 7\\&b= 20 \sqrt 7\\&\\&\\&\text{Para calcular la altura planteamos estas dos ecuaciones}\\&\text{siendo d la base del triangulos rectángulo que forma a}\\&\\&h^2 = a^2-d^2\\&h^2= b^2-(70-d)^2\\&\\& a^2-d^2= b^2-(70-d)^2\\&700 - d^2=2800 - (70-d)^2\\&700 - d^2=2800-4900-d^2+140d\\&140d = 700-2800+4900\\&140d = 2800\\&d=20\\&\\&h^2=a^2-d^2 = 700-400 = 300\\&h= 10 \sqrt 3\\&\end{align}$$:
: