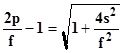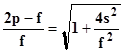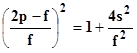Pueden explicarme cómo despejar esta la variable en esta fórmula matemática.
Pueden explicarme cómo despejar esta fórmula, se despejar pero en esta tengo la variable dentro de una raíz, envío el ejercicio en una imagen.
La variable a despejar es ( es ) y esta dentro de la raíz cuadrada que hay adentro de los paréntesis.
Gracias.

2 Respuestas
Respuesta de Luis Alberto Candio Salcedo
1
Respuesta de Valero Angel Serrano Mercadal