¿Cómo resolver un ejercicio con integrales dobles?
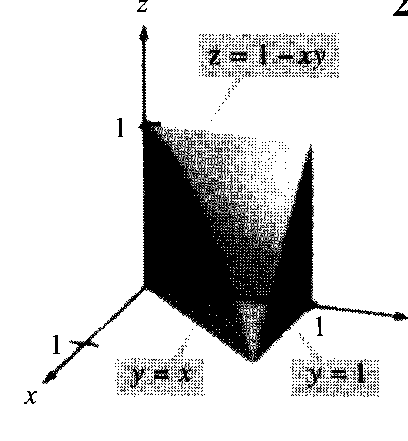
Usar una integral doble para calcular el volumen del sólido siguiente
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
2
---
¡Hola Francisco!
·
Los límites en y son [0, 1]
como son fijos son los que conviene poner en la integral de fuera.
En x el dominio está entre el eje Y que es x=0 y la recta x=y,
luego son [0, y]
Y el volumen es:
$$\begin{align}&V=\iint_Dz(x,y) \;dx\,dy\\&\\&V=\int_0^1\int_0^y(1-xy)\;dx\,dy=\\&\\&\int_0^1\left[x+\frac{x^2y}{2} \right]_0^y dy=\\&\\&\int_0^1 \left(y+\frac{y^3}{2} \right)dy=\\&\\&\left[\frac{y^2}{2}+\frac{y^4}{8} \right]_0^1=\frac{1}{2}+\frac 18=\frac{4+1}{8}=\frac 58\end{align}$$Y eso es todo.
