Cual es la imagen de lineas horizontales y verticales bajo

·

Dado un punto

z=a+bi

tendremos

$$\begin{align}&\cos(a+ib) = \cos a·cosh\, b-sen\,a·senh\,b\end{align}$$

Es algo que tendrás en la teoría o en ejercicios, recientemente he constestado preguntas sobre esto.  Ahora veo que era una pregunta tuya precisamente

http://www.todoexpertos.com/preguntas/5xq4jexeym4yoeya/variable-compleja-sobre-forma-binomica?selectedanswerid=5xq8y5kwypg4ffn4

Si la recta es horizontal tiene por ecuación

y=k

y los puntos son (t, k) para todo t de R

la transformación en el plano uv será

$$\begin{align}&u=\cos \,t·cosh\,k\\&v= sen \,t·senh \,k\\&\\&\text {Esto es una elipse centrada en el origen}\\&\\&\frac{u}{cosh\,k}=\cos t\\&\\&\frac{v}{senh \,k}=sen\,t\\&\\&\text{elvándolas al cuadrado y su}\text{mándolas}\\&\\&\frac{u^2}{cosh^2k}+\frac{v^2}{senh^2k}=1\\&\\&\\&\text{Si es una recta vertical x=k}\\&\text{tiene los puntos (k,t) }\forall t \in \mathbb R\\&\\&u=\cos \,k·cosh\,t\\&v= sen \,k·senh \,t\\&\\&\text{que es una hipérbola}\\&\\&\frac{u}{cosk}= cosh\,t\\&\\&\frac{v}{senk}=senh\,t\\&\\&\text {elevanto al cuadrado y restando}\\&\\&\frac{u^2}{\cos^2k}-\frac{v^2}{sen^2k}=cosh^2t-senh^2t=1\end{align}$$

Y la gráfica sería esta.  Nótese que una recta veertical se tranforma en las dos ramas de la hipérbola, no solo en una.

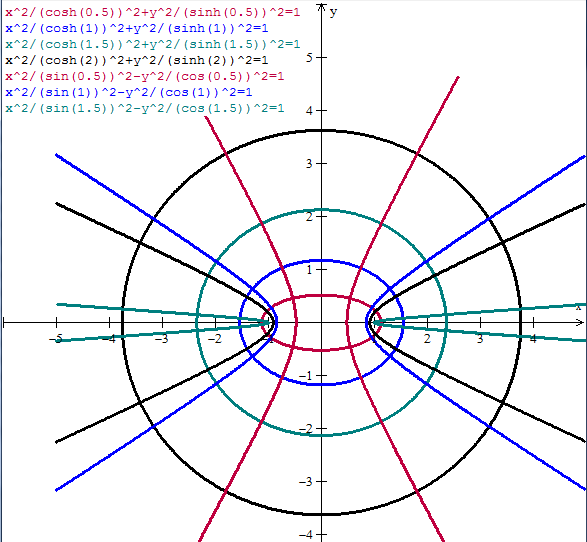
Y eso es todo.