Anónimo
Verificar el siguiente limite usando la definición de limite de una función vectorial
$$\begin{align}&\\&\lim_{t \to \ 2} f ⃗(t)=(6,4) \ si f(t) = 3t i+t^2 j\end{align}$$
2 Respuestas
·
La definición de límite de una función vectorial es:
Dada una función vectorial,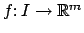 
, 
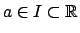un punto de acumulación (es decir, que hay puntos del dominio tan cerca de 
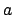como queramos), y 
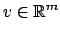, decimos que 
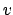es el límite de 
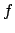cuando 
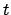tiende a , 
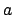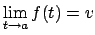, si ocurre que
·
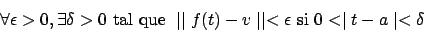
La norma será la de la raíz cuadrada de la suma de los cuadrados
$$\begin{align}&||f(t)-v||=\sqrt{(3t-6)^2+(t^2-4)^2}=\\&\\&\text{Usamos el producto notable}\\&\\&a^2-b^2=(a-b)(a+b)\\&\\&\text{y sacamos un factor común}\\&\\&=\sqrt{9(t-2)^2+[(t-2)(t+2)]^2}=\\&\\&=|t-2| ·\sqrt{9+(t+2)^2}\end{align}$$Sea cual sea el epsilon que nos den, tomaremos un delta con valor máximo 1, ellos nos permite hacer una primera acotación de la raíz cuadrada que constituye el segundo factor.
La función 9+(t+2)^2 es una parábola hacia arriba con el vértice en t=-2, luego si tomamos un entorno de radio 1 en t=2, que es el entorno (1, 3) estamos en la rama creciente de la parábola y el valor máximo que tomará es
9+(3+2)^2 = 9+25 = 34
luego el máximo valor que tomará la raíz cuadrada es:
$$\begin{align}&\sqrt {34}\\&\\&\text{Luego tomando incialmente }\delta=1\\&\text{si }0\lt|t-2|\lt \delta=1\\&\\&||f(t)-(6,4)||=\\&\\&|t-2| \sqrt{9+(t+2)^2}\lt 1·\sqrt {34} = \sqrt{34}\\&\\&Si\; \epsilon\ge \sqrt {34}\;\text{ tomaremos }\delta=1\\&\\&\text{pero lo que importa es cuando }\epsilon \lt \sqrt {34}\\&\\&\text{Si }0\lt|t-2|<\delta\\&\\&||f(t)-(6,4)||\lt \sqrt{34}· |t-2|\lt\sqrt{ 34} \delta\le\epsilon\implies\\&\\&\sqrt{ 34} \delta\le\epsilon\implies \delta\le \frac{\epsilon}{\sqrt{34}}\\&\\&\text{Luego si tomamos}\\&\\&\delta=min \left\{1,\frac{\epsilon}{\sqrt{34}} \right\}\quad y\quad 0\lt|t-2|\lt\delta\implies\\&\\&||f(t)-(6,4)||\lt\epsilon\\&\\&\text{por lo tanto}\\&\\&\lim_{t\to 2}f(t)=(6,\,4)\end{align}$$·
Y eso es todo.
Simplemente tomas limites para cada componente del vector:
Vx= 3t .para t tendiendo a 2 ..................6
Vy = t^2 .........para t tendiendo a 2 .......4
Luedo vector limite para t tendiendo a 2 = (6, 4)