¿Como Graficar la Curva f(x)=x^3-4x?

·

Derivaremos la función y la igualaremos a 0 para calcular los puntos críticos

f(x) = x^3 - 4x

f '(x) = 3x^2 - 4 =0

3x^2 = 4

x^2 = 4/3

Los dos puntos críticos son:

$$\begin{align}&x_1=\sqrt{\frac 43}=\frac{2}{\sqrt 3}=\frac{2 \sqrt 3}{3}\\&\\&x_2=-\sqrt{\frac 43}=-\frac{2}{\sqrt 3}=-\frac{2 \sqrt 3}{3}\\&\end{align}$$

El último paso se llama racionalizar denominadores, me ha sido realmente útil una o dos veces en mi vida y un millón de veces no ha valido para nada, pero a los profesores les encanta que lo hagas.

Para saber si son máximos o mínimos usaremos bien el criterio de la derivada segunda u otros.

Con la derivada segunda

f''(x) = 6x

Con lo cual el punto critico negativo dara negativo y es un máximo y el positivo dará positivo y es un mínimo.

Y la otra forma es que al tratarse de un polinomio de grado 3 con coeficiente director positivo empieza en -infinito y crece hasta el primer punto crítico que es el negativo, por lo tanto es un máximo, luego decrece hasta el otro punto crítico positivo que será un mínimo y finalmente crece hasta el infinito.

Vamos a calcularlos este máximo y minimo para tener dos puntos de la gráfica que poder pintar

$$\begin{align}&-\frac{2 \sqrt 3}{3}\approx -1.154700538379252\\&\\&f\left(-\frac{2 \sqrt 3}{3}  \right)=-\frac{8·3·\sqrt 3}{27}+4·\frac{2 \sqrt 3}{3}=\\&\\&-\frac{8}{9}\sqrt 3+\frac{8}{3}\sqrt 3=-\frac{8}{9}\sqrt 3+\frac{24}{9}\sqrt 3=\\&\\&\frac{16}{9}\sqrt 3\approx 3.079201435678004\end{align}$$

Para dibujar el punto quédate como mucho que el máximo es

(-1.15,  3.08)

Y el otro punto se calcula de forma parecida y el mínimo es

(1.15, -3.08)

Esto me sugiere que la función tiene simetría central

f(-x) = -f(x)

veamos

f(-x) = (-x)^3 -4(-x) = -x^3 + 4x = -f(x)   es verdad

Y los periodos de crecimiento o decrecimiento los marcan los máximos o mínimos.

Antes de un máximo crecen y después decrecen, y antes de un mínimo decrecen y luego crecen

Que haya dos puntos críticos sugiere que pueda haber un punto de inflexión, vemos si se anula la derivada segunda

f''(x) = 6x =0

x=0

Lo lógico y normal en una fución de simetria central, que el 0 sea punto de inflexión, es el punto (0,0) antes del cero la derivada segunda es negativa, luego concava hacia abajo que es forma de iglú y despues del cero es cóncava hacia arriba que es forma de U.

Y con todo esto y alguna cosa más como algunos puntos extras se podría dibujar y queda

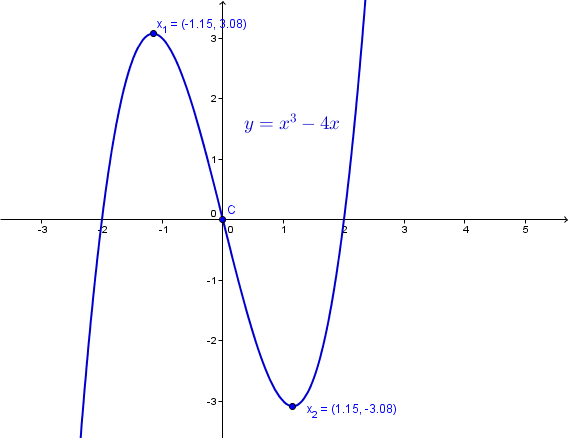
Y eso es todo.

Te dejo la imagen de la función, graficada para x entre -30 y 50.

Respecto a máximos y mínimos, para esto hay que calcular su derivada, luego tenemos que

$$\begin{align}&f(x) = x^3-4x\\&f'(x)=3x^2-4\\&f'(x)=0 \rightarrow x=\pm \sqrt{{4 \over 3}}\\&Para \;  ver \; si \; los \; puntos \; criticos \; son \; maximos \; o \; minimos, \; calculamos \; f''(x), \; luego\\&f''(x)=6x\\&f''(-\sqrt{4\over3}) < 0 \rightarrow maximo\\&f''(+\sqrt{4\over3}) > 0 \rightarrow minimo\\&\end{align}$$