Desarrolle este problema por favor de DINAMICA y ayudeme con la grafica. Gracias fv

Enrique Et!

Este es un ejercicio apropiado, no tendrían porque ser más difíciles que este, aun me echa humo la cabeza y el ordenador esta hiperventilando del ejercicio anterior que dejé.

Empezamos por el apartado b y seguido el a

$$\begin{align}&v(t)=\int20\,sen\,2t\;dt = -10cos 2t + C\\ &     \\ &     \text{como v(10)=5 m/s}\\ &     \\ &     v(10)=-10cos(2·10) +C = 5\\ &     \\ &     C=5+10\,\cos 20\\ &     \\ &     v(t)=-10cos2t+5+10\,\cos 20\\ & \\ &     v(t)=-10cos2t + 9.08082\\ &     \\ &     \\ &     x(t)=\int(-10cos2t + 9.08082)dt=\\ &     -5sen\,2t+ 9.08082t+C\\ &     \\ &     \text{Como x(10)=0 m}\\ &     \\ &     x(10)=-5sen20+9.08082·10+C=0\\ &     \\ &     C= 5sen 20-90.8082= -86.24348\\ &    \\ &    x(t)=-5sen\,2t+ 9.08082t-86.24348\end{align}$$

c)

En el punto 3 tendremos

x(3) = -5sen6 + 9.08082·3 - 86.24348 = -57.60394 m

v(3) = -10cos6 +9.08082 = -0.52088 m/s

a(3) = 20sen6 = -5.58831 m/s^2

d)  Ya hemos calculado la posición en 3, ahora calculamos en 8

x(8) = -5sen(16) + 9.08082·8 - 86.24348 = -12.15740 m

La distancia recorrida es

x(8) - x(3) = 45.44654 m

e)

Y las gráficas son estas:

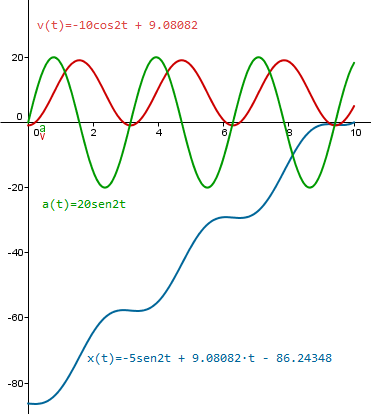
Y eso es todo.

¡Gracias! Experto podría ayudarme con este otro ejercicio porque no se puede enviar

Una Acotación los temas que llevo son Cinemática del punto y Movimiento Rectilíneo

Si se puede aplicar integrales explique me

Gracias

Gracias