Operaciones con espacios vectoriales
En R², con la métrica usual d2, considera los siguientes conjuntos:
C = {(x, y)|x² + x² <=1} L = {(x,y)|x + y =2}
a) calcula d2(C, L)
b) Traza los dos conjuntos en un plano cartesiano e ilustra geométricamente.
1 respuesta
Creo que has tenido una errata al escribir el conjunto C, supongo que es
C={(x,y) | x^2+y^2 <=1}
La distancia es el ínfimo de las distancias entre dos pares de puntos de uno y otro conjunto.
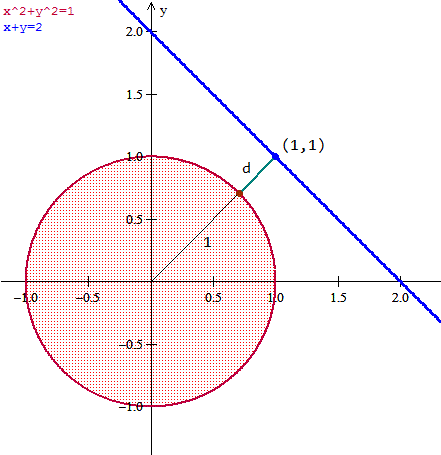
C es la circunferencia de radio 1, L es una recta que hace un triángulo rectángulo con los ejes en el primer cuadrante pasando por los puntos (2,0) y (0,2), los ángulos no rectos son de 45 grados. El punto más cercano entre recta y circunferencia es el dado por los puntos que están en perpendicular a la recta pasando por el centro.
Para la recta es el punto (1,1) y para la circunferencia es el
(cos45, sen45)= (sqrt(2)/2, sqrt(2)/2)
La distancia es
$$\begin{align}&\sqrt{\left(1-\frac{\sqrt 2}{2}\right)^2+\left(1-\frac{\sqrt 2}{2}\right)^2}=\\ &\\ &\\ &\sqrt{2\left(\frac{2-\sqrt 2}{2}\right)^2}=\frac{2-\sqrt 2}{2}\sqrt 2 =\\ &\\ &\frac{2 \sqrt 2-2}{2}= \sqrt 2 -1 \end{align}$$b)
Y eso es todo.
